[LeetCode] Max Points on a Line 共线点个数

Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.

Example 1:

Input: [[1,1],[2,2],[3,3]]
Output: 3
Explanation:
^
|
|        o
|     o
|  o  
+------------->
0  1  2  3  4

Example 2:

Input: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4
Explanation:
^
|
|  o
|     o        o
|        o
|  o        o
+------------------->
0  1  2  3  4  5  6

这道题给了我们一堆二维点，然后让求最大的共线点的个数，根据初中数学可以知道，两点确定一条直线，而且可以写成 y = ax + b 的形式，所有共线的点都满足这个公式。所以这些给定点两两之间都可以算一个斜率，每个斜率代表一条直线，对每一条直线，带入所有的点看是否共线并计算个数，这是整体的思路。但是还有两点特殊情况需要考虑，一是当两个点重合时，无法确定一条直线，但这也是共线的情况，需要特殊处理。二是斜率不存在的情况，由于两个点 (x1, y1) 和 (x2, y2) 的斜率k表示为 (y2 - y1) / (x2 - x1)，那么当 x1 = x2 时斜率不存在，这种共线情况需要特殊处理。这里需要用到 TreeMap 来记录斜率和共线点个数之间的映射，其中第一种重合点的情况假定其斜率为 INT_MIN，第二种情况假定其斜率为 INT_MAX，这样都可以用 TreeMap 映射了。还需要顶一个变量 duplicate 来记录重合点的个数，最后只需和 TreeMap 中的数字相加即为共线点的总数，但这种方法现在已经无法通过 OJ 了，代码可以参见评论区八楼。

由于通过斜率来判断共线需要用到除法，而用 double 表示的双精度小数在有的系统里不一定准确，为了更加精确无误的计算共线，应当避免除法，从而避免无线不循环小数的出现，那么怎么办呢，这里把除数和被除数都保存下来，不做除法，但是要让这两数分别除以它们的最大公约数，这样例如8和4，4和2，2和1，这三组商相同的数就都会存到一个映射里面，同样也能实现目标，而求 GCD 的函数如果用递归来写那么一行就搞定了，叼不叼，这个方法能很好的避免除法的出现，算是牺牲了空间来保证精度吧，参见代码如下：

C++ 解法一：

class Solution {
public:
    int maxPoints(vector<vector<int>>& points) {
        int res = ;
        for (int i = ; i < points.size(); ++i) {
            map<pair<int, int>, int> m;
            int duplicate = ;
            for (int j = i + ; j < points.size(); ++j) {
                if (points[i][] == points[j][] && points[i][] == points[j][]) {
                    ++duplicate; continue;
                }
                int dx = points[j][] - points[i][];
                int dy = points[j][] - points[i][];
                int d = gcd(dx, dy);
                ++m[{dx / d, dy / d}];
            }
            res = max(res, duplicate);
            for (auto it = m.begin(); it != m.end(); ++it) {
                res = max(res, it->second + duplicate);
            }
        }
        return res;
    }
    int gcd(int a, int b) {
        return (b == ) ? a : gcd(b, a % b);
    }
};

Java 解法一：

class Solution {
    public int maxPoints(int[][] points) {
        int res = 0;
        for (int i = 0; i < points.length; ++i) {
            Map<Map<Integer, Integer>, Integer> m = new HashMap<>();
            int duplicate = 1;
            for (int j = i + 1; j < points.length; ++j) {
                if (points[i][0] == points[j][0] && points[i][1] == points[j][1]) {
                    ++duplicate; continue;
                }
                int dx = points[j][0] - points[i][0];
                int dy = points[j][1] - points[i][1];
                int d = gcd(dx, dy);
                Map<Integer, Integer> t = new HashMap<>();
                t.put(dx / d, dy / d);
                m.put(t, m.getOrDefault(t, 0) + 1);
            }
            res = Math.max(res, duplicate);
            for (Map.Entry<Map<Integer, Integer>, Integer> e : m.entrySet()) {
                res = Math.max(res, e.getValue() + duplicate);
            }
        }
        return res;
    }
    public int gcd(int a, int b) {
        return (b == 0) ? a : gcd(b, a % b);
    }
}

令博主惊奇的是，这道题的 OJ 居然容忍 brute force 的方法通过，博主认为下面这种 O(n³) 的解法之所以能通过 OJ，可能还有一个原因就是用了比较高效的判断三点共线的方法。一般来说判断三点共线有三种方法，斜率法，周长法，面积法 (请参见这个帖子)。而其中通过判断叉积为零的面积法是坠好的。比如说有三个点 A(x1, y1)、B(x2, y2)、C(x3, y3)，那么判断三点共线就是判断下面这个等式是否成立：

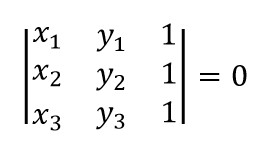
行列式的求法不用多说吧，不会的话回去翻线性代数，当初少打点刀塔不就好啦~

C++ 解法二：

class Solution {
public:
    int maxPoints(vector<vector<int>>& points) {
        int res = ;
        for (int i = ; i < points.size(); ++i) {
            int duplicate = ;
            for (int j = i + ; j < points.size(); ++j) {
                int cnt = ;
                long long x1 = points[i][], y1 = points[i][];
                long long x2 = points[j][], y2 = points[j][];
                if (x1 == x2 && y1 == y2) {++duplicate; continue;}
                for (int k = ; k < points.size(); ++k) {
                    int x3 = points[k][], y3 = points[k][];
                    if (x1 * y2 + x2 * y3 + x3 * y1 - x3 * y2 - x2 * y1 - x1 * y3 == ) {
                        ++cnt;
                    }
                }
                res = max(res, cnt);
            }
            res = max(res, duplicate);
        }
        return res;
    }
};

Java 解法二：

class Solution {
    public int maxPoints(int[][] points) {
        int res = 0, n = points.length;
        for (int i = 0; i < n; ++i) {
            int duplicate = 1;
            for (int j = i + 1; j < n; ++j) {
                int cnt = 0;
                long x1 = points[i][0], y1 = points[i][1];
                long x2 = points[j][0], y2 = points[j][1];
                if (x1 == x2 && y1 == y2) {++duplicate;continue;}
                for (int k = 0; k < n; ++k) {
                    int x3 = points[k][0], y3 = points[k][1];
                    if (x1*y2 + x2*y3 + x3*y1 - x3*y2 - x2*y1 - x1 * y3 == 0) {
                        ++cnt;
                    }
                }
                res = Math.max(res, cnt);
            }
            res = Math.max(res, duplicate);
        }
        return res;
    }
}

Github 同步地址：

https://github.com/grandyang/leetcode/issues/149

类似题目：

Line Reflection

参考资料：

https://leetcode.com/problems/max-points-on-a-line/

https://leetcode.com/problems/max-points-on-a-line/discuss/221044/

https://leetcode.com/problems/max-points-on-a-line/discuss/47113/A-java-solution-with-notes

https://leetcode.com/problems/max-points-on-a-line/discuss/47117/Sharing-my-simple-solution-with-explanation

LeetCode All in One 题目讲解汇总(持续更新中...)