Java数据结构之堆和优先队列

概述

在谈堆之前，我们先了解什么是优先队列。我们每天都在排队，银行，医院，购物都得排队。排在队首先处理事情，处理完才能从这个队伍离开，又有新的人来排在队尾。但仅仅这样就能满足我们生活需求吗，明显不能。医院里，患者排队准备看病，这时有个重症患者入队，医生如果按队列的方式一个一个往下处理，等排到这位重病患者时，可能他就因为伤情过重挂了，之后就会引发医患纠纷，这明显不是我们想要的结果。优先队列就成为我们解决此类事情的关键，重病患者入队（挂号），医生根据他的伤情紧急（优先级）优先处理他的病情。

如果非要用专业术语来区分他们二者的区别

1. 队列先进先出，后进后出
2. 优先队列，出队与入队时的顺序无关，与优先级有关。

堆

了解了优先队列，那这个堆又是什么玩意，可能很多人听过内存堆栈。特别要声明和注意的是，这里的堆仅仅是存储数据的一种结构方式，与内存的堆栈不是一个概念。

1. 二叉堆是一颗完全二叉树结构（不懂什么是树的同学请面壁），说的通俗点，堆就是满足一些特殊性质的树，所以二叉堆就是有特殊性质的二叉树。
2. 父节点的值大于（小于）两个子节点的值，又称为最大堆和最小堆，我们要定义的是最大堆（最小堆跟他相反）。

实例

我们先来看下什么是满的二叉树

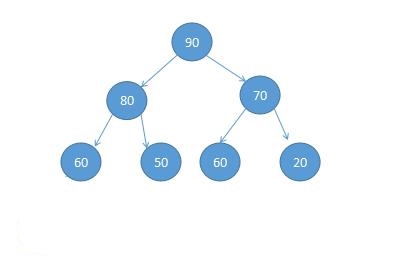
每一层所有节点都有两个儿子结点的二叉树，就叫满的二叉树，计算他节点个数的公式2^3 - 1 = 7。有七个节点

完全二叉树（最大堆）

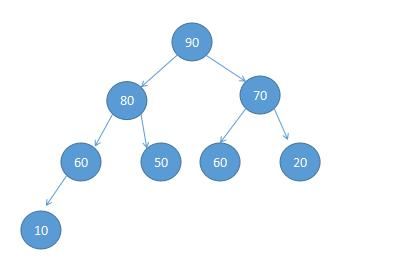
堆和优先队列有什么关系

知道了什么是堆和优先队列，它们之间有什么关系哪。说穿了就一句话，堆是优先队列这种数据结构的一种实现方式。

注意：优先队列可以用不同的底层实现（普通线性结构），时间复杂度不同。

数组实现完全二叉树（最大堆）

也可以定义二叉树来实现完全二叉树，但是通过观察会发现其结构的特点，都是用顺序存储方式存储。从1到n编号，就得到结点的一个线性系列。每一层结点个数恰好是上一层结点个数的2倍，也因此通过一个节点的编号就可以推知他的左右孩子节点的编号。

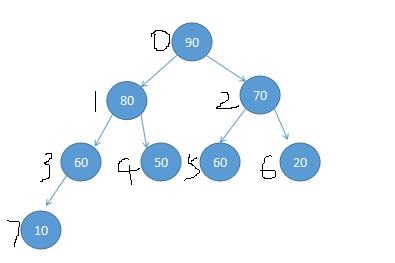
通过分析和数学归纳得出一个结论，很方便的知道他的左右孩子节点和父节点。

1. 父节点 parent(i) = （i - 1） / 2，算下结点10的父节点 (7 - 1) / 2 = 3 就是 60
2. 左孩子 left child(i) = 2 * i + 1，可以算出 10 的左孩子 7 * 2 + 1 = 15 > 7 (这里的7为最大索引值)没有左孩子这个结点
3. 右孩子 right child(i) = 2 * i + 2,可以算出 10 的右孩子 7 * 2 + 2 = 16 > 7 没有右孩子这个结点

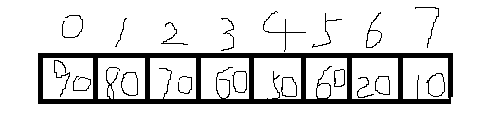
定义一个我们自己的数组Array类，也可以用Java提供的Array

Array类

public class Array<E> {
 
    private E[] data;
 
    private int size;
 
    //构造函数，传入数组的容量capacity构造Array
    public Array(int capacity) {
        this.data = (E[]) new Object[capacity];
        size = 0;
    }
//无参数构造函数
    public Array() {
        this(10);
    }
 
    //获取数组的个数
    public int getSize() {
        return size;
    }
 
    //获取数组的容量
    public int getCapacity() {
        return data.length;
    }
 
    //数组是否为空
    public boolean isEmpty() {
        return size == 0;
    }
 
    //添加最后一个元素
    public void addLast(E e) {
        add(size,e);
    }
 
    //添加第一个元素
    public void addFirst(E e){
        add(0,e);
    }
 
    //获取inde索引位置的元素
    public E get(int index){
        if (index < 0 || index >= size){
            throw new IllegalArgumentException("Get failed,index is illegal");
        }
        return data[index];
    }
 
    public void set(int index,E e){
        if (index < 0 || index >= size){
            throw new IllegalArgumentException("Get failed,index is illegal");
        }
        data[index] =  e;
    }
 
    //获取最后一个元素
    public E getLast(){
        return this.get(size - 1);
    }
 
    //获取第一个元素
    public E getFirst(){
        return this.get(0);
    }
 
    //添加元素
    public void add(int index,E e){
        if (index > size || index < 0){
            throw new IllegalArgumentException("add failed beceause index > size or index < 0,Array is full.");
        }
        if (size == data.length){
            resize(data.length * 2);
        }
        for (int i = size - 1; i >= index; i--) {
            data[i+1] = data[i];
        }
        data[index] = e;
        size ++;
 
    }
 
    //扩容数组
    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newData[i] = data[i];
        }
        data = newData;
    }
 
    public E[] getData() {
        return data;
    }
 
    //查找数组中是否有元素e
    public boolean contains(E e){
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e)){
                return true;
            }
        }
        return false;
    }
 
    //根据元素查看索引
    public int find(E e){
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e)){
                return i;
            }
        }
        return -1;
    }
 
    //删除某个索引元素
    public E remove(int index){
        if(index < 0 || index >= size){
            throw new IllegalArgumentException("detele is fail,index < 0 or index >= size");
        }
        E ret = data[index];
        for (int i = index + 1; i < size; i++) {
            data[i - 1] = data[i];
        }
        size --;
        data[size] = null;
        if (size < data.length / 2){
            resize(data.length / 2);
        }
        return  ret;
    }
 
    //删除首个元素
    public E removeFirst(){
        return this.remove(0);
    }
 
    //删除最后一个元素
    public E removeLast(){
        return this.remove(size - 1);
    }
 
    //从数组删除元素e
    public void removeElemen(E e){
        int index = find(e);
        if (index != -1){
            remove(index);
        }
 
    }
 
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder("");
        sb.append(String.format("Array:size = %d,capacity = %d \n",size,data.length));
        sb.append("[");
        for (int i = 0; i < size; i++) {
            sb.append(data[i]);
            if (i != size - 1){
                sb.append(",");
            }
        }
        sb.append("]");
        return sb.toString();
    }
}

有了Array数组类，接下来很快的，把我们刚才描述的事情用代码实现出来之后，在考虑出队和入队的操作，因为父节点要大于或小于他们的子节点。所以我们的节点要能相互比较，在Java继承Comparable类就可以了。

最大堆（MaxHeap类）

public class MaxHeap<E extends Comparable<E>>
{
    private Array<E> data;
 
    public MaxHeap(int capacity)
    {
        data = new Array<>(capacity);
    }
 
    public MaxHeap()
    {
        data = new Array<>();
    }
 
    //堆里的元素个数
    public int size()
    {
        return data.getSize();
    }
 
    //堆是否为空
    public boolean isEmpty()
    {
        return data.isEmpty();
    }
 
    //根据一个元素的索引，获取他父亲索引
    private int parent(int index)
    {
        if (index == 0)
        {
            throw new IllegalArgumentException("index - 0 does't have parent.");
        }
        return (index - 1) / 2;
    }
 
    //根据一个元素的索引，获取他右孩子的索引
    private int leftChild(int index)
    {
 
        return index * 2 + 1;
    }
 
    //根据一个元素的索引，获取他左孩子的索引
    private int rightChild(int index)
    {
        return index * 2 + 2;
    }
 
}

向堆中添加一个元素，在堆的内部要进行一个上浮的操作，保证用数组实现的二叉堆还符合我们最大堆的性质（父节点的值大于两个子节点的值）。

82大于他的父节点60，两个结点交换位置，82还大于他的父结点80，两个节点交换位置。80小于现在的父结点90，结束交换。这个操作很多人称为上浮操作（个人认为名称贴切）上浮操作完成。

用代码实现我们刚才的操作，已经知道他父结点的位置（公式），交换两个人的位置就变得很简单，MaxHeap添加函数。

    //堆中添加元素
    public void add(E e)
    {
        data.addLast(e);
        siftUp(data.getSize() - 1);
    }
 
    //上浮操作
    private void siftUp(int i)
    {
        while (i > 0 && data.get(parent(i)).compareTo(data.get(i)) < 0)
        {
            //交换位置
            data.swap(i,parent(i));
　　　　　　　i = parent（i）
        }
    }

Array类，添加交换位置的函数

    public void swap(int i,int j)
    {
        if (i < 0 || i >= size || j < 0 || j > size)
        {
            throw new IllegalArgumentException("索引越界");
        }
        E t = data[i];
        data[i] = data[j];
        data[j] = t;
 
    }

有添加就有取出，取出堆中元素其实很简单，因为最大堆决定了只取堆顶元素（数组的第一个元素），直接取出即可。困难的是如何维护二叉堆的性质不变。

取出堆顶元素后

取出堆顶元素，剩下两个子树，将两颗子树糅合成一个二叉堆，现在直接将60这个元素作为堆顶，就满足了完全二叉树的性质但并不符合最大堆性质。

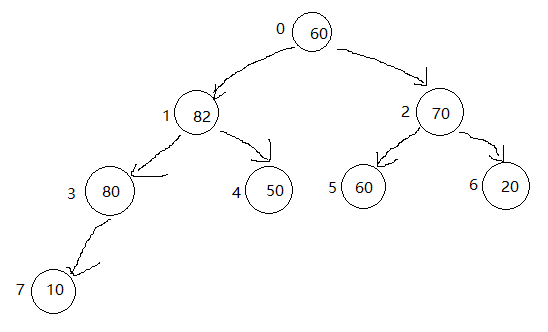
和上浮的操作相反，现在我们要进行下沉的操作，60的左右孩子都比60来得大，要选择左右孩子最大的那个数进行交换，82和60进行交换，80比60来得大，交换他们的位置，10比60来得小，符合二叉堆的性质。交换结束。

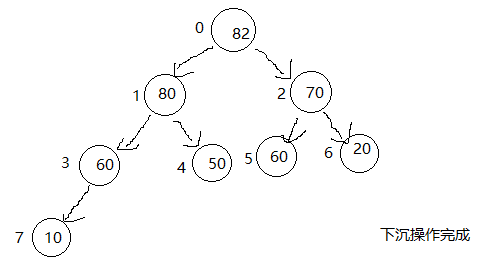
用代码描述刚才取出的操作。

MaxHeap类

    //堆中最大元素
    public E findMax()
    {
        if (data.getSize() == 0)
        {
            throw new IllegalArgumentException("堆为空，无法查看值");
        }
        return data.get(0);
    }
    //取出堆顶元素
    public E extractMax()
    {
        E ret = findMax();
        data.swap(0,data.getSize() - 1);
        data.removeLast();
        siftDown(0);
        return ret;
    }
 
    //下沉操作
    private void siftDown(int i)
    {
        //比较到他左右孩子那个比他大进行交换操作
        while (leftChild(i) < data.getSize())
        {
            int j = leftChild(i);
            if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) //右节点
            {
                j = rightChild(i);
            }
            if (data.get(i).compareTo(data.get(j)) >= 0)
            {
                break;
            }
            data.swap(i,j);
            i = j;
        }
    }

现在我们堆结构基本完成，简单测试一下

Main类

public class Main
{
    public static void main(String[] args) {
        MaxHeap<Integer> maxHeap = new MaxHeap<>();
        int[] nums = {90,80,70,60,50,60,20,10};
        for (int i = 0; i < nums.length; i++)
        {
            maxHeap.add(nums[i]);
        }
        System.out.println("堆顶:" + maxHeap.findMax());
        maxHeap.add(82);//添加82
        System.out.println("取出堆顶值:" + maxHeap.extractMax());
        System.out.println("堆顶:" + maxHeap.findMax());//是否为82
        maxHeap.add(85);//添加85
        System.out.println("堆顶:" + maxHeap.findMax()); //是否为85
        System.out.println("测试结束");
    }
}

输出

堆顶:90
取出堆顶值:90
堆顶:82
堆顶:85
测试结束

用定义的最大堆去实现一个优先队列就变得十分简单了，优先队列本质上来说还是一个队列，用堆来实现队列的接口。

Queue接口类

public interface Queue<E> {
 
    int getSize();
 
    boolean isEmpty();
 
    void enqueue(E e);
 
    E dequeue();
 
    E getFront();
}

优先队列（PriorityQueue类）

public class PriorityQueue<E extends Comparable<E>> implements Queue<E>
{
    private MaxHeap<E> maxHeap;
 
    public PriorityQueue()
    {
        maxHeap = new MaxHeap<>();
    }
 
    @Override
    public int getSize() {
        return maxHeap.size();
    }
 
    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }
 
    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }
 
    @Override
    public E dequeue() {
        return maxHeap.extractMax();
    }
 
    @Override
    public E getFront() {
        return maxHeap.findMax();
    }
}

实例

在股票市场，很多股民向股票代理打电话，股票代理公司优先处理vip客户（有钱￥）再处理普通的用户。把他们的money当做他们的优先程度

Customer类

public class Customer implements Comparable<Customer> {
    private int money;
 
    private String name;
 
    public Customer(int money, String name) {
        this.money = money;
        this.name = name;
    }
 
    public int getMoney() {
        return money;
    }
 
    public void setMoney(int money) {
        this.money = money;
    }
 
    public String getName() {
        return name;
    }
 
    public void setName(String name) {
        this.name = name;
    }
 
    @Override
    public int compareTo(Customer another) {
        if (this.money < another.money)
        {
            return -1;
        }else if (this.money > another.money)
        {
            return 1;
        }else {
            return 0;
        }
    }
}

Main类

public class Main
{
    public static void main(String[] args) {
        //优先队列使用示例
        Queue<Customer> queue = new PriorityQueue<>();
        Random random = new Random();
        for (int i = 0; i < 10; i++)
        {
            int money = random.nextInt(1000000);
            queue.enqueue(new Customer(money,"客户" + i ));
        }
        while (true)
        {
            if (queue.isEmpty())
            {
                break;
            }
            Customer customer = queue.dequeue();
            System.out.println("优先处理 " + customer.getName() + " 因为他的money为:" + customer.getMoney() + "￥");
        }
    }
 
}

输出

优先处理 客户4 因为他的money为:842917￥
优先处理 客户7 因为他的money为:628183￥
优先处理 客户8 因为他的money为:578457￥
优先处理 客户0 因为他的money为:551270￥
优先处理 客户1 因为他的money为:538859￥
优先处理 客户5 因为他的money为:297316￥
优先处理 客户3 因为他的money为:262908￥
优先处理 客户9 因为他的money为:250763￥
优先处理 客户6 因为他的money为:144102￥
优先处理 客户2 因为他的money为:96273￥

随机数，输出结果不确定。但一定是从大到小排序，如果要从小到大很简单，改比较符即可。这边实现的是最大堆，Java提供的优先队列（PriorityQueue）底层是最小堆。

============================================

如发现错误请留言提醒lz，好及时修改，避免误导别人。拜谢