使用LINGO来解决0/1背包算法问题
1.问题说明
0/1背包问题:我们有n种物品,物品j的重量为wj,价格为pj。我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为W。如果限定每种物品只能选择0个或1个,则问题称为0-1背包问题。(摘自百度百科)
例子:
假设有10个物品,重量和价格分别如下图所示,背包承受最大重量W=2000,每种物品能选择放或者不放,求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
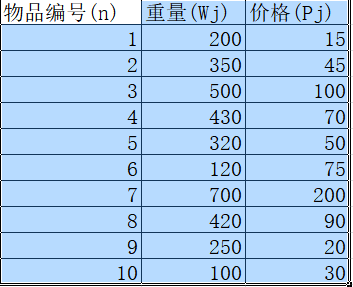
2.数学模型

3.lingo代码实现
需要用到的特性是lingo的集合,数据,函数

4.效果
点击solve按钮,即可求得所有的未知数。

由图可知,isok为1的数的号码,为了获得最大值我们所需要放入背包的物品是:3号,6号,7号,8号,10号。
此时的背包内物品的总重量是1840,总价值是495.
源码地址:https://files.cnblogs.com/files/lizhijian/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%AE%97%E6%B3%95.rar
感谢阅读
使用LINGO来解决0/1背包算法问题的更多相关文章
- 非对称加密RSA、Elgamal、背包算法、Rabin、D-H、ECC(椭圆曲线加密算法)等。使用最广泛的是RSA算法
非对称加密算法需要两个密钥:公开密钥(publickey)和私有密钥(privatekey).公开密钥与私有密钥是一对,如果用公开密钥对数据进行加密,只有用对应的私有密钥才能解密:如果用私 ...
- poj1417 带权并查集+0/1背包
题意:有一个岛上住着一些神和魔,并且已知神和魔的数量,现在已知神总是说真话,魔总是说假话,有 n 个询问,问某个神或魔(身份未知),问题是问某个是神还是魔,根据他们的回答,问是否能够确定哪些是神哪些是 ...
- 决策树之ID3、C4.5、C5.0等五大算法
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- C5.0决策树之ID3.C4.5.C5.0算法 ...
- 设子数组A[0:k]和A[k+1:N-1]已排好序(0≤K≤N-1)。试设计一个合并这2个子数组为排好序的数组A[0:N-1]的算法。
设子数组A[0:k]和A[k+1:N-1]已排好序(0≤K≤N-1).试设计一个合并这2个子数组为排好序的数组A[0:N-1]的算法.要求算法在最坏情况下所用的计算时间为O(N),只用到O(1)的辅助 ...
- P1417 烹调方案 (0/1背包+贪心)
题目背景 由于你的帮助,火星只遭受了最小的损失.但gw懒得重建家园了,就造了一艘飞船飞向遥远的earth星.不过飞船飞到一半,gw发现了一个很严重的问题:肚子饿了~ gw还是会做饭的,于是拿出了储藏的 ...
- 洛谷 P1064 金明的预算方案 (有依赖的0/1背包)
题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间.更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过NN元钱就行”. ...
- POJ 1636 Prison rearrangement DFS+0/1背包
题目链接: id=1636">POJ 1636 Prison rearrangement Prison rearrangement Time Limit: 3000MS Memor ...
- POJ 1745 【0/1 背包】
题目链接:http://poj.org/problem?id=1745 Divisibility Time Limit: 1000MS Memory Limit: 10000K Total Sub ...
- Hash冲突的解决--暴雪的Hash算法
Hash冲突的解决--暴雪的Hash算法https://usench.iteye.com/blog/2199399https://www.bbsmax.com/A/kPzOO7a8zx/
随机推荐
- 笔记:MyBatis XML配置详解
MyBatis 的配置文件包含了影响 MyBatis 行为甚深的设置(settings)和属性(properties)信息.文档的顶层结构如下: configuration 配置 properties ...
- python统计词频
arr = [1,2,3,4,5,6,4,5,2,3,6,8,9,6,5,3,6,2,4]dic={}for item in arr: if item in dic.keys(): dic[item] ...
- POJ-1032-拆数字
Description New convocation of The Fool Land's Parliament consists of N delegates. According to the ...
- Linux chown命令
chown将指定文件的拥有者改为指定的用户或组,用户可以是用户名或者用户ID:组可以是组名或者组ID:文件是以空格分开的要改变权限的文件列表,支持通配符.系统管理员经常使用chown命令,在将文件拷贝 ...
- Spark核心技术原理透视一(Spark运行原理)
在大数据领域,只有深挖数据科学领域,走在学术前沿,才能在底层算法和模型方面走在前面,从而占据领先地位. Spark的这种学术基因,使得它从一开始就在大数据领域建立了一定优势.无论是性能,还是方案的统一 ...
- JS时间处理由CST格式转成GMT格式时间
问题描述:js接收java后台的时间数据时,时间格式的CST时间,而js默认的是GMT时间格式,js 需要对这个时间进行处理才能使用,具体处理方法如function dateToGMT(sDate){ ...
- 【HTML】 HTML基础知识 表单
html 表单 表单的标签是<form>,用于给网站的后台提交数据.提交的数据格式原本是什么样不太清楚,以python的flask框架来看,我从表单中得到的数据是一个字典(flask.re ...
- Oracle查询优化改写--------------------范围处理
一.定位连续值的范围 二.查找同一组或分区中行之间的差
- Python中的classmethod与staticmethod
首先,这是一个经典的问题. 我们首先做一个比较: classmethod的第一个参数是cls,即调用的时候要把类传入 这意味着我们我们可以在classmethod里使用类的属性,而不是类的实例的属性( ...
- 剑指Offer-二叉树的下一个结点
题目描述 给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回.注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针. 思路 分析二叉树的下一个节点,一共有以下情况: 二叉树 ...
