[BZOJ]1071 组队(SCOI2007)

　　一道比较NB的套路题。

Description

　　NBA每年都有球员选秀环节。通常用速度和身高两项数据来衡量一个篮球运动员的基本素质。假如一支球队里速度最慢的球员速度为minV，身高最矮的球员高度为minH，那么这支球队的所有队员都应该满足: A * ( height – minH ) + B * ( speed – minV ) <= C 其中A和B，C为给定的经验值。这个式子很容易理解，如果一个球队的球员速度和身高差距太大，会造成配合的不协调。请问作为球队管理层的你，在N名选秀球员中，最多能有多少名符合条件的候选球员。

Input

　　第一行四个数N、A、B、C 下接N行每行两个数描述一个球员的height和speed。

Output

　　最多候选球员数目。

Sample Input

　　4 1 2 10
　　5 1
　　3 2
　　2 3
　　2 1

Sample Output

HINT

　　1 <= N <= 5000，0<= height,speed <= 10000，A、B、C在长整型以内且为正数。

Solution

　　最暴力的O(n^3)做法就是枚举minH和minV，加入满足条件的点即可。

　　我们试着优化一下：

　　一看到n=5000，肯定是n^2的做法，因此我们有枚举minH和minV其中一个的余地，所以还是枚举minV，把speed[i]<minV的点去除。

　　然后我们把式子转化一下：

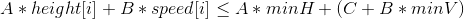
　　由于我们枚举了minV，所以minV可以看做是一个常数，设C'=C+B*minV。

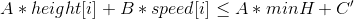
　　这就很有意思，我们设X[i]=height[i]，Y[i]=A*height[i]+B*speed[i]。于是每个运动员就对应平面直角坐标系中的点(X[i],Y[i])。

　　当我们枚举minH的时候，就相当于在问有多少个点(X[i],Y[i])满足：

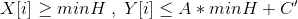　　　　，这就是一个二维数点问题。

　　把这些点按照X[i]排序从大到小加点，用(离散化加上)树状数组维护Y[i]，就可以得到一个O(n^2logn)的做法。

　　虽然时间复杂度爆炸但是小C才不会告诉你小C用这个做法过了该题。

　　但是我们注意到随着minH的减小，A*minH+C'也是不断减小的，(A>0，虽然原题没说但是就算A为负数也是同理的做法)。

　　所以我们把这些点不仅按X[i]排序，还要按Y[i]排序，用两个指针维护，按X[i]从大到小加点，并按Y[i]从大到小删点。

　　再加上我们对这些点使用排序时用上插入排序，就可以得到一个O(n^2)的做法。

#include <cstdio>

#include <cstring>

#include <algorithm>

#define ll long long

#define MN 5003

using namespace std;

struct meg{int x,z; ll y;}a[MN];

int c1[MN],c2[MN];

bool u[MN];

int n,A,B,C,ans,tp1,tp2;

inline int read()

{

    int n=,f=; char c=getchar();

    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}

    while (c>='' && c<='') {n=n*+c-''; c=getchar();}

    return n*f;

}

void solve(ll CX)

{

    register int i,j,k,sum=;

    ll lt;

    for (i=tp1,k=tp2;i;i=j)

    {

        lt=1LL*A*a[c1[i]].x+CX;

        for (j=i;j&&a[c1[j]].x==a[c1[i]].x;--j)

            if (a[c1[j]].y<=lt) ++sum,u[c1[j]]=true;

        for (;k&&a[c2[k]].y>lt;--k)

            if (u[c2[k]]) --sum,u[c2[k]]=false;

        ans=max(ans,sum);

    }

    for (;k;--k) if (u[c2[k]]) u[c2[k]]=false;

}

void isort1(int ax)

{

    register int i,j;

    for (i=;i<=tp1;++i)

        if (a[ax].x<a[c1[i]].x) break;

    ++tp1;

    for (j=tp1;j>i;--j) c1[j]=c1[j-];

    c1[i]=ax;

}

void isort2(int ax)

{

    register int i,j;

    for (i=;i<=tp2;++i)

        if (a[ax].y<a[c2[i]].y) break;

    ++tp2;

    for (j=tp2;j>i;--j) c2[j]=c2[j-];

    c2[i]=ax;

}

bool cmp1(const meg& a,const meg& b) {return a.z<b.z;}

int main()

{

    register int i,j;

    n=read(); A=read(); B=read(); C=read();

    for (i=;i<=n;++i)

    {

        a[i].x=read(); a[i].z=read();

        a[i].y=1LL*a[i].x*A+1LL*a[i].z*B;

    }

    sort(a+,a+n+,cmp1);

    for (i=n;i;i=j)

    {

        for (j=i;j&&a[j].z==a[i].z;--j)

            isort1(j),isort2(j);

        solve(1LL*a[i].z*B+C);

    }

    printf("%d",ans);

}

Last Word

　　小C的O(n^2logn)做法（BZOJ上总时限为3s）：

　　O(n^2)做法（对比）：

　　常数小就是舒服.jpg