Prim算法(一)之 C语言详解

本章介绍普里姆算法。和以往一样，本文会先对普里姆算法的理论论知识进行介绍，然后给出C语言的实现。后续再分别给出C++和Java版本的实现。

目录
1. 普里姆算法介绍
2. 普里姆算法图解
3. 普里姆算法的代码说明
4. 普里姆算法的源码

转载请注明出处：http://www.cnblogs.com/skywang12345/

更多内容：数据结构与算法系列 目录

普里姆算法介绍

普里姆(Prim)算法，和克鲁斯卡尔算法一样，是用来求加权连通图的最小生成树的算法。

基本思想
对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。
从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

普里姆算法图解

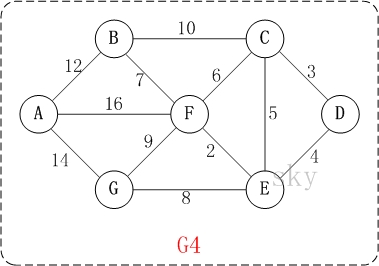
以上图G4为例，来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。

初始状态：V是所有顶点的集合，即V={A,B,C,D,E,F,G}；U和T都是空！
第1步：将顶点A加入到U中。
    此时，U={A}。
第2步：将顶点B加入到U中。
    上一步操作之后，U={A}, V-U={B,C,D,E,F,G}；因此，边(A,B)的权值最小。将顶点B添加到U中；此时，U={A,B}。
第3步：将顶点F加入到U中。
    上一步操作之后，U={A,B}, V-U={C,D,E,F,G}；因此，边(B,F)的权值最小。将顶点F添加到U中；此时，U={A,B,F}。
第4步：将顶点E加入到U中。
    上一步操作之后，U={A,B,F}, V-U={C,D,E,G}；因此，边(F,E)的权值最小。将顶点E添加到U中；此时，U={A,B,F,E}。
第5步：将顶点D加入到U中。
    上一步操作之后，U={A,B,F,E}, V-U={C,D,G}；因此，边(E,D)的权值最小。将顶点D添加到U中；此时，U={A,B,F,E,D}。
第6步：将顶点C加入到U中。
    上一步操作之后，U={A,B,F,E,D}, V-U={C,G}；因此，边(D,C)的权值最小。将顶点C添加到U中；此时，U={A,B,F,E,D,C}。
第7步：将顶点G加入到U中。
    上一步操作之后，U={A,B,F,E,D,C}, V-U={G}；因此，边(F,G)的权值最小。将顶点G添加到U中；此时，U=V。

此时，最小生成树构造完成！它包括的顶点依次是：A B F E D C G。

普里姆算法的代码说明

以"邻接矩阵"为例对普里姆算法进行说明，对于"邻接表"实现的图在后面会给出相应的源码。

1. 基本定义

// 邻接矩阵
typedef struct _graph
{
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。
EData是邻接矩阵边对应的结构体。

2. 普里姆算法

/*
 * prim最小生成树
 *
 * 参数说明：
 *       G -- 邻接矩阵图
 *   start -- 从图中的第start个元素开始，生成最小树
 */
void prim(Graph G, int start)
{
    int min,i,j,k,m,n,sum;
    int index=0;         // prim最小树的索引，即prims数组的索引
    char prims[MAX];     // prim最小树的结果数组
    int weights[MAX];    // 顶点间边的权值

    // prim最小生成树中第一个数是"图中第start个顶点"，因为是从start开始的。
    prims[index++] = G.vexs[start];

    // 初始化"顶点的权值数组"，
    // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
    for (i = 0; i < G.vexnum; i++ )
        weights[i] = G.matrix[start][i];
    // 将第start个顶点的权值初始化为0。
    // 可以理解为"第start个顶点到它自身的距离为0"。
    weights[start] = 0;

    for (i = 0; i < G.vexnum; i++)
    {
        // 由于从start开始的，因此不需要再对第start个顶点进行处理。
        if(start == i)
            continue;

        j = 0;
        k = 0;
        min = INF;
        // 在未被加入到最小生成树的顶点中，找出权值最小的顶点。
        while (j < G.vexnum)
        {
            // 若weights[j]=0，意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
            if (weights[j] != 0 && weights[j] < min)
            {
                min = weights[j];
                k = j;
            }
            j++;
        }

        // 经过上面的处理后，在未被加入到最小生成树的顶点中，权值最小的顶点是第k个顶点。
        // 将第k个顶点加入到最小生成树的结果数组中
        prims[index++] = G.vexs[k];
        // 将"第k个顶点的权值"标记为0，意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
        weights[k] = 0;
        // 当第k个顶点被加入到最小生成树的结果数组中之后，更新其它顶点的权值。
        for (j = 0 ; j < G.vexnum; j++)
        {
            // 当第j个节点没有被处理，并且需要更新时才被更新。
            if (weights[j] != 0 && G.matrix[k][j] < weights[j])
                weights[j] = G.matrix[k][j];
        }
    }

    // 计算最小生成树的权值
    sum = 0;
    for (i = 1; i < index; i++)
    {
        min = INF;
        // 获取prims[i]在G中的位置
        n = get_position(G, prims[i]);
        // 在vexs[0...i]中，找出到j的权值最小的顶点。
        for (j = 0; j < i; j++)
        {
            m = get_position(G, prims[j]);
            if (G.matrix[m][n]<min)
                min = G.matrix[m][n];
        }
        sum += min;
    }
    // 打印最小生成树
    printf("PRIM(%c)=%d: ", G.vexs[start], sum);
    for (i = 0; i < index; i++)
        printf("%c ", prims[i]);
    printf("\n");
}

普里姆算法的源码

这里分别给出"邻接矩阵图"和"邻接表图"的普里姆算法源码。

1. 邻接矩阵源码(matrix_udg.c)

2. 邻接表源码(list_udg.c)