7. ensemble learning & AdaBoost

1. ensemble learning 集成学习

集成学习是通过构建并结合多个学习器来完成学习任务，如下图：

集成学习通过将多个学习学习器进行结合，常可以获得比单一学习器更优秀的泛化性能

从理论上来说，使用“弱学习器”集成足以获得好的性能，当实践中出于种种考虑，人们往往会使用比较强的学习器。

以下面为例，集成学习的结构通过投票法Voting（少数服从多数）产生：

由上面可以看出：个体学习器应该“好而不同”，即个体学习器要有一定的“准确性”，并且彼此间要有差异。

从理论上来说，假设个体学习器的误差 $\epsilon$ 相互独立，那么随着集成中个体分类器数目 $T$ 的增加，集成的错误率将呈指数级下降。但现实任务中，个体学习器是为解决同一个问题而训练出来的，它们显然不可能相互独立。

根据个体学习器的生成方式，目前的集成学习方法大致分为两大类：
1. 个体学习器间存在强依赖关系，必须串行生成的序列化方法，如 Boosting
2. 个体学习器间不存在强依赖关系，可同时生成并行化方法，如Bagging 和 Random Forest

2. Boposting & AdaBoost

Boosting: 先从初始训练集训练一个基学习器，再根据学习器的表现对训练样本分布进行调整，使得先前基类学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此反复进行，直至基学习器达到事先指定值$T$，最终将这$T$个基学习器进行加权结合。

Boosting族算法中最著名的代表就是AdaBoost。

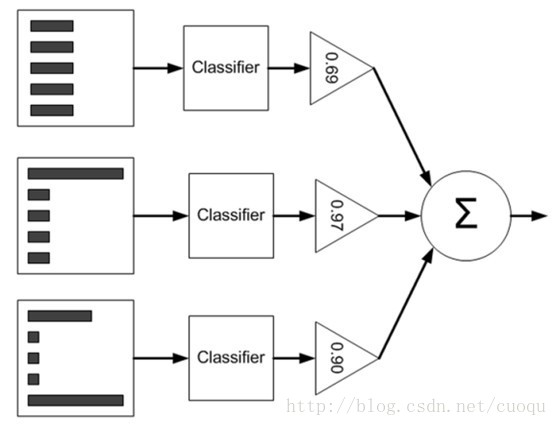
这是AdaBoost的原理示意图：左边矩形表示数据集$D$，中间是各个个体学习器，右边三角形是对每个弱学习器赋予的权重 $\alpha$ ，最后根据每个弱学习器的加权组合来判断总体类别。要注意一下数据集从上到下三个矩形内直方图不一样，这表示每个样本的权重 $\mathcal{D}$ 也发生了变化，样本的权重一开始初始化为相等的权重，然后根据弱学习器的错误率 $\epsilon$ 来调整每个弱学习器的权重 $\alpha$以及样本权重 $\mathcal{D}$.

具体过程如下：

The error $\epsilon$ is given by
$\epsilon = \frac{number of incorrectly classified examples}{total number of examples}$

and $\alpha$ is given by
$\alpha = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})$

$\mathcal{D}_{t+1,i} = \frac{\mathcal{D}_{t,i}}{Z_t} {\times} e^{-\alpha_t f(x_i) h_t(x_i)}$

$Z_t = \sum_{i=1}^{m}\mathcal{D}_{t,i} {\times} e^{-\alpha_t f(x_i) h_t(x_i)}$

1、弱分类器的选取

弱分类器的选取并没有一个特定的标准或选取准则，一般来说只要是能够实现基本的分类功能的分类器均可以作为adaboost中的弱分类器。

2、分类误差大于0.5，终止算法

分类误差大于0.5代表当前的分类器是否比随机预测要好，对于一个随机预测模型来说，其分类误差就是0.5，即一半预测对，一半预测错。若当前的弱分类器还没有随机预测的效果好，那便直接终止算法。但是当adaboost遇到这种情形时可能学习的迭代次数远远没有达到初始设置的迭代次数M，这可能会导致最终集成中只有很少的弱分类器，从而导致算法整体性能不佳。为了化解这种情况Kohavi在《Bias plus variance decomposition for zero-one loss functions》提出了用重采样法使得迭代过程重新启动。

参考：

周志华机器学习

http://blog.csdn.net/sinat_17451213/article/details/51055718

http://blog.csdn.net/marvin521/article/details/9319459

http://blog.csdn.net/autocyz/article/details/51305999