2sum问题求解

什么是2sum问题呢？举个例子就明白了：对于数列：【0、1、2、3、4、5、6、7、8、9】，求两数相加=9的所有两数的组合，所以结果为：【0、9】,【1、8】,【2、7】,【3、6】,【4、5】。所以就是要在一组数据中将结果全部输出出来，说到两个数相加等于某一个数，那也有可能是三个数、四个数相加呀，所以说其实这个问题可以归纳为ksum问题，只不过咱们先从2sum最基础的开始接触。

如何实现呢？这里用两种方式来实现，时间复杂度分别为O(n^2)和O(n)，可见第一种是最基础的实现，好理解，但是性能不太高；而第二种则是对其进行进一步优化的，下面开始：

O(n^2)实现：

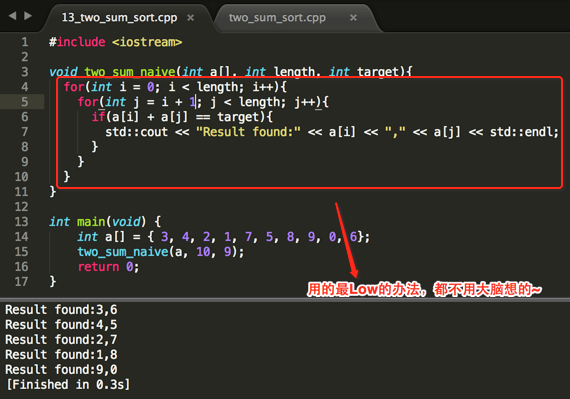
这里就不多解释了，小朋友都能理解~~

O(n)线性级别超高性能的优化实现：

这种高效的实现方式有个前提：是一个排好序的数组。所以如果在面试的时候可以跟面试官沟通是否可以对数组进行排序来达到求解的目的，如果是的话那这种方式就完美可以回答了，那如果面试官不让排序也能达到O(n)级别的高性能优化实现呢？在之后也会有一个方法能达到，这里先来学习下通过排序达到目的的解法。

思路：

对于上面这个有序的数列中，找出两数相加=9的所有组合，可以这样：

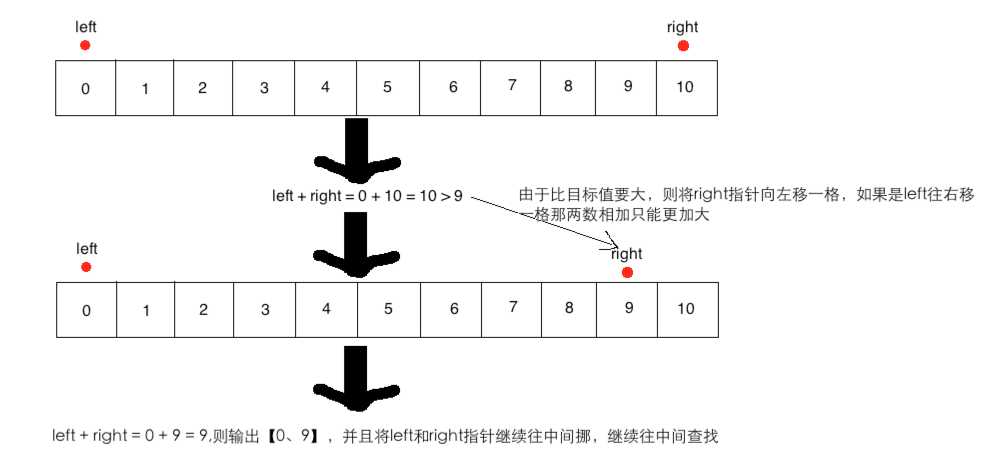
思路总结：

1、如果left + right > 目标值，则right--;

2、如果left + right < 目标值, 则left++;

3、如果left == right，则输出数组，然后将left++、right--继续往中间去找寻。

是不是思路so easy~下面看代码：

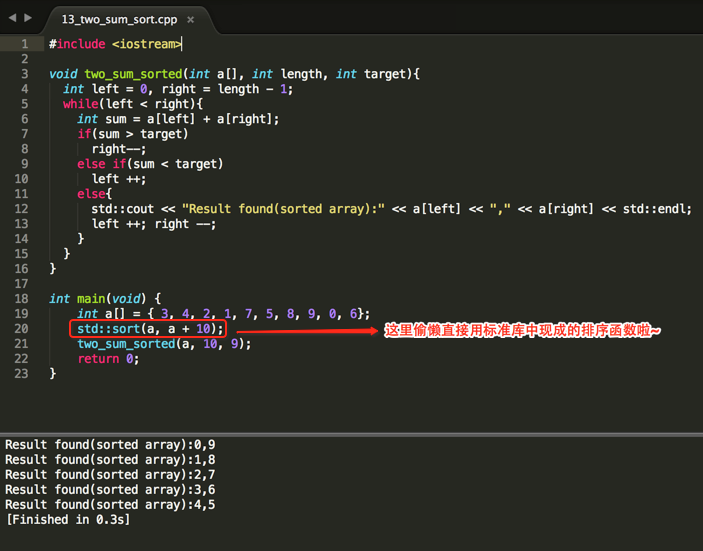
程序不多解释了，一看就懂！