Leetcode题目46.全排列（回溯+深度优先遍历+状态重置-中等）

题目描述：

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

题目解析：来自leetcode@liweiwei1419

以示例输入: [1, 2, 3] 为例，如果让我们手写，要做到不重不漏，我们书写的策略可能是这样：“一位一位确定”，这样说比较笼统，具体是这样的：

1、先写以 1 开始的两个排列：[1, 2, 3]、[1, 3, 2]；
2、再写以 2 开始的两个排列：[2, 1, 3]、[2, 3, 1]；
3、最后写以 3 开始的两个排列：[3, 1, 2]、[3, 2, 1]。

如果数组元素多一点的话，也不怕，我们写的时候遵循下面的原则即可：

1、按数组的顺序来（不要求排序，但我们选取元素的顺序是从左到右的），每次排定 1 个元素；
说明：只有按照顺序才能做到不重不漏。

2、新排定的元素一定不能在之前排定的元素中出现。
说明：如果违反了这一条，就不符合“全排列”的定义。

其实让程序帮你找到所有的全排列也是这样的思路。如果不是这样的话，我们要写数组长度这么多层的循环，编码极其困难，代码写出来也非常不好看。

这道题可以作为理解“回溯算法”的入门题。这是一个非常典型的使用 回溯算法 解决的问题。解决回溯问题，我的经验是 一定不要偷懒，拿起纸和笔，把这个问题的递归结构画出来，一般而言，是一个树形结构，这样思路和代码就会比较清晰了。而写代码即是将画出的图用代码表现出来。

思路分析：

方法：“回溯搜索”算法即“深度优先遍历 + 状态重置 + 剪枝”（这道题没有剪枝）
以示例输入: [1, 2, 3] 为例，因为是排列问题，只要我们按照顺序选取数字，保证上一层选过的数字不在下一层出现，就能够得到不重不漏的所有排列。

说明：这里“保证上一层选过的数字不在下一层出现”的意思是我们手写的时候，后面选的数字一定不能是前面已经出现过的。为了做到这一点，我们得使用一个数组长度这么长的额外空间，记为数组 used ，只要“上一层”选了一个元素，我们就得“标记一下”，“表示占位”。

画出树形结构如下图，

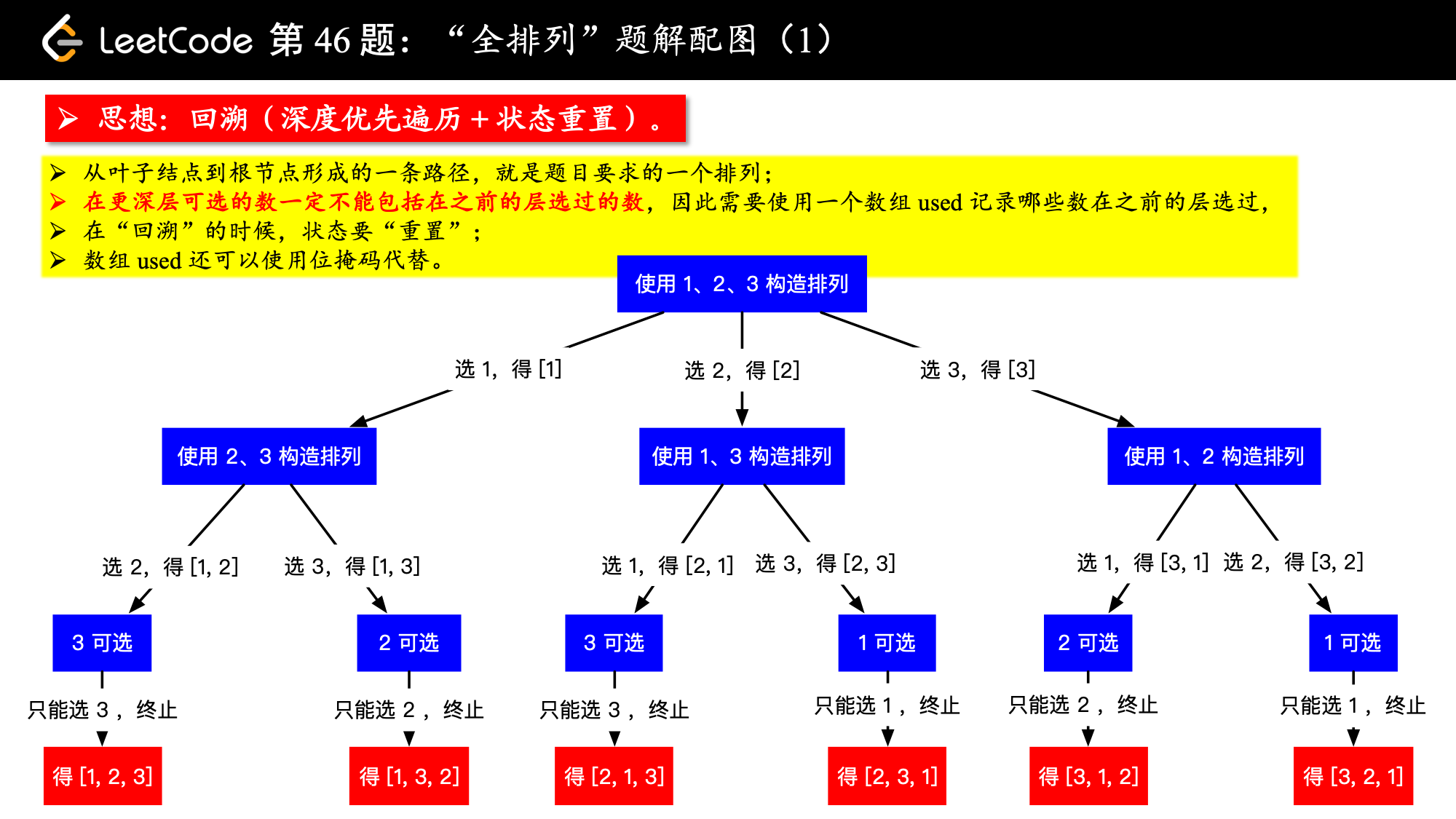
这里我们介绍什么是“状态”。

在递归树里，辅助数组 used 记录的情况和当前已经选出数组成的一个排序，我们统称为当前的“状态”。

注意：

1、这里特别说明一点：虽然我的图是一下子展示出来的，但是我想你画出的图应该是一层一层画出来的；

2、在每一层，我们都有若干条分支供我们选择。下一层的分支数比上一层少 1 ，因为每一层都会排定 1 个数，从这个角度，再来理解一下为什么要使用额外空间记录那些元素使用过；

3、全部的“排列”正是在这棵递归树的所有叶子结点。

我们把上面这件事情给一个形式化的描述：问题的解空间是一棵递归树，求解的过程正是在这棵递归树上搜索答案，而搜索的路径是“深度优先遍历”，它的特点是“不撞南墙不回头”。

下面解释“状态重置”。

在程序执行到上面这棵树的叶子结点的时候，此时递归到底，当前根结点到叶子结点走过的路径就构成一个全排列，把它加入结果集，我把这一步称之为“结算”。此时递归方法要返回了，对于方法返回以后，要做两件事情：

（1）释放对最后一个数的占用；
（2）将最后一个数从当前选取的排列中弹出。

事实上在每一层的方法执行完毕，即将要返回的时候都需要这么做。这棵树上的每一个结点都会被访问 2 次，绕一圈回到第 1 次来到的那个结点，第 2 次回到结点的“状态”要和第 1 次来到这个结点时候的“状态”相同，这种程序员赋予程序的操作叫做“状态重置”。

“状态重置”是“回溯”的重要操作，“回溯搜索”是有方向的搜索，否则我们要写多重循环，代码量不可控。

说明：

1、数组 used 记录了索引 i 在递归过程中是否被使用过，还可以用哈希表、位图来代替，在下面的参考代码 2 和参考代码 3 分别提供了 Java 的代码；

2、当程序第 1 次走到一个结点的时候，表示考虑一个数，要把它加入列表，经过更深层的递归又回到这个结点的时候，需要“状态重置”、“恢复现场”，需要把之前考虑的那个数从末尾弹出，这都是在一个列表的末尾操作，最合适的数据结构是栈（Stack）。

请大家在脑子里想一想程序在这棵递归树上“深度优先遍历”执行的路径，理解了“状态重置”这个概念，是不是觉得“回溯搜索”这个名字很形象。

如果序列包含重复数字，这就是 「力扣」第 47 题：“全排列 II”，需要做“剪枝”操作，做法可以参考《回溯 + 剪枝（Python 代码、Java 代码）》。

参考代码 1 是全排列问题我个人觉得比较好的写法，可以作为写回溯算法的模板，类似的问题写出来的代码基本都是这个样子。

代码实现：

package com.company;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

/**
 * @author yaoshw
 */
public class Main {

    public static void main(String[] args) {

        int[] nums = new int[]{1, 2, 3};
        List<List<Integer>> result = permute(nums);
        result.forEach(System.out::println);
    }

    public static List<List<Integer>> permute(int[] nums) {

        int len = nums.length;
        List<List<Integer>> result = new ArrayList<>();

        if (len == 0) {
            return result;
        }
        boolean[] used = new boolean[len];
        generatePermute(nums, used, 0, len, new Stack<>(), result);
        return result;

    }

    /**
     * @param nums    输入的数组
     * @param visited 标记某一位是否在当前搜索中被访问的状态
     * @param curSize 当前索引，即搜索在哪一层了
     * @param len     数组的长度
     * @param path    一次搜索的结果集，即一条路径上的值的组合
     * @param result  全排列
     * @return 数组内元素的全排列
     */
    private static void generatePermute(int[] nums, boolean[] visited, int curSize, int len, Stack<Integer> path, List<List<Integer>> result) {

        if (curSize == len) {
            result.add(new ArrayList<>(path));
        }
        for (int i = 0; i < len; i++) {
            //当前值没有被访问时，将其加入到当前序列中
            if (!visited[i]) {
                path.push(nums[i]);
                visited[i] = true;
                generatePermute(nums, visited, curSize + 1, len, path, result);
                //回溯前后，状态重置
                path.pop();
                visited[i] = false;
            }
        }
    }

}

时间复杂度：O(∑ k=1N​ P(N,k))， P(N, k) = {N!}{(N - k)!} = N (N - 1) ... (N - k + 1)，该式被称作 n 的 k-排列，或者_部分排列。

空间复杂度：O(N!) 由于必须要保存N!个解。