[题解] [ZJOI2014] 力

题面

题解

恩, 我们首先有这两个关系

\[\displaystyle\begin{aligned} F_j &= \sum_{i < j}\frac{q_iq_j}{(i - j)^2} - \sum_{i > j}\frac{q_iq_j}{(i - j)^2}\\ &= q_j\cdot(\sum_{i < j}\frac{q_i}{(i - j)^2}-\sum_{i>j}\frac{q_i}{(i - j)^2})\end{aligned}
\]

然后由

\[\displaystyle E_i = \frac{F_i}{q_i}
\]

我们可以推出这样的式子

\[\displaystyle\begin{aligned}
E_i&=\frac{F_i}{q_i}\\&=\sum_{j<i}\frac{q_j}{(i - j)^2}-\sum_{j>i}\frac{q_j}{(j - i)^2}\\
\end{aligned}
\]

我们来看一下 n = 3 的情况

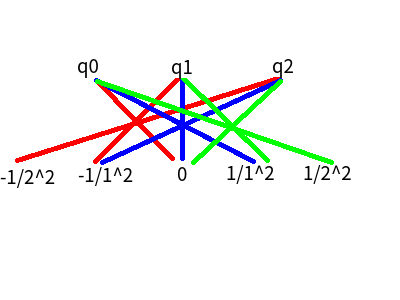
我们将红色的线的两端乘起来, 再把三条红线的和相加就得到了\(E_0\), 同理我们通过蓝线, 绿线可以得到\(E_1\), \(E_2\)

我们定义\(a_i = p_i\), \(b_i = \frac{1}{i ^ 2}\), 特别的, 我们定义\(b_{-i} = -\frac{1}{i ^ 2}\), 先别管为什么下标为负

\[\displaystyle\begin{aligned}
E_0&=a_0b_0+a_1b_{-1}+a_2b_{-2}\\
E_1&=a_0b_1+a_1b_0+a_2b_{-1}\\
E_2&=a_0b_2+a_1b_1+a_2b_0
\end{aligned}
\]

恩, 我们来讨论数组下标小于零的问题, 整体平移就行了嘛, 注意到\(b\)最小的下标为\((-3 + 1)\), 所以我们平移\((3 - 1)\)位就可以了, 所以有:

\[\begin{aligned}
E_0&=a_0b_2+a_1b_1+a_2b_0\Leftrightarrow E_0 = \sum_{i+j=2}a_ib_j\\
E_1&=a_0b_3+a_1b_2+a_2b_1\Leftrightarrow E_1 = \sum_{i+j=3}a_ib_j\\
E_2&=a_0b_4+a_1b_3+a_2b_2\Leftrightarrow E_2 = \sum_{i+j=4}a_ib_j
\end{aligned}
\]

恩, 我们来看一下卷积的形式

\[c_k = \sum_{i + j = k}a_ib_j
\]

我们会发现这里的\(E\)数组的下标离可以卷积差了一个\((3 - 1)\), 用\(E_2\)代替\(E_0\)就可以用\(a\)与\(b\)的卷积来算了

我们将特殊情况扩展到一般情况, 设\(E\)共有\(n\)项, 自己瞎猜一下可以发现\(b\)数组下标平移了\(n - 1\)位, \(E\)数组的下标平移了\(n - 1\)位, 所以, 最后我们输出\(E\)的第\([n - 1, (n - 1) + n - 1]\)项即可

这篇题解就是写给我们这种蒟蒻看的, 至于卷积, 我猜各位是为了练习FFT才来做这道题的吧

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <cmath>
#define itn int
#define reaD read
#define N 1000005
const double pi = acos(-1);
using namespace std;

int n, m, cnt, rev[N];
struct complex
{
	double x, y;
	complex(double xx = 0, double yy = 0) { x = xx; y = yy; }
	complex operator + (complex p) { return complex(x + p.x, y + p.y); }
	complex operator - (complex p) { return complex(x - p.x, y - p.y); }
	complex operator * (complex p) { return complex(x * p.x - y * p.y, x * p.y + y * p.x); }
} a[N], b[N]; 

inline int read()
{
	int x = 0, w = 1; char c = getchar();
	while(c < '0' || c > '9') { if (c == '-') w = -1; c = getchar(); }
	while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
	return x * w;
}

void FFT(complex* p, int opt)
{
	for(int i = 0; i < m; i++) if(i < rev[i]) swap(p[i], p[rev[i]]);
	for(int i = 1; i < m; i <<= 1)
	{
		complex cur = complex(cos(pi / i), opt * sin(pi / i));
		for(int j = 0; j < m; j += (i << 1))
		{
			complex w = complex(1, 0);
			for(int k = 0; k < i; k++, w = w * cur)
			{
				complex l = p[j + k], r = w * p[i + j + k];
				p[j + k] = l + r; p[i + j + k] = l - r;
			}
		}
	}
}

int main()
{
	n = read();
	for(int i = 0; i < n; i++) scanf("%lf", &a[i].x);
	for(int i = 1; i < n; i++)
	{
		b[i + n - 1].x = 1 / (1.0 * (double) i * i);
		b[n - 1 - i].x = -b[i + n - 1].x;
	}
	for(m = 1; m <= 3 * n - 2; m <<= 1, cnt++);
	for(int i = 0; i < m; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	FFT(a, 1); FFT(b, 1);
	for(int i = 0; i <= m; i++) a[i] = a[i] * b[i];
	FFT(a, -1);
	for(int i = n - 1; i <= 2 * n - 2; i++) printf("%.3lf\n", a[i].x / m);
	return 0;
}

这可能是我写得最认真的一篇题解吧, 希望看这篇题解的泥萌可以康懂