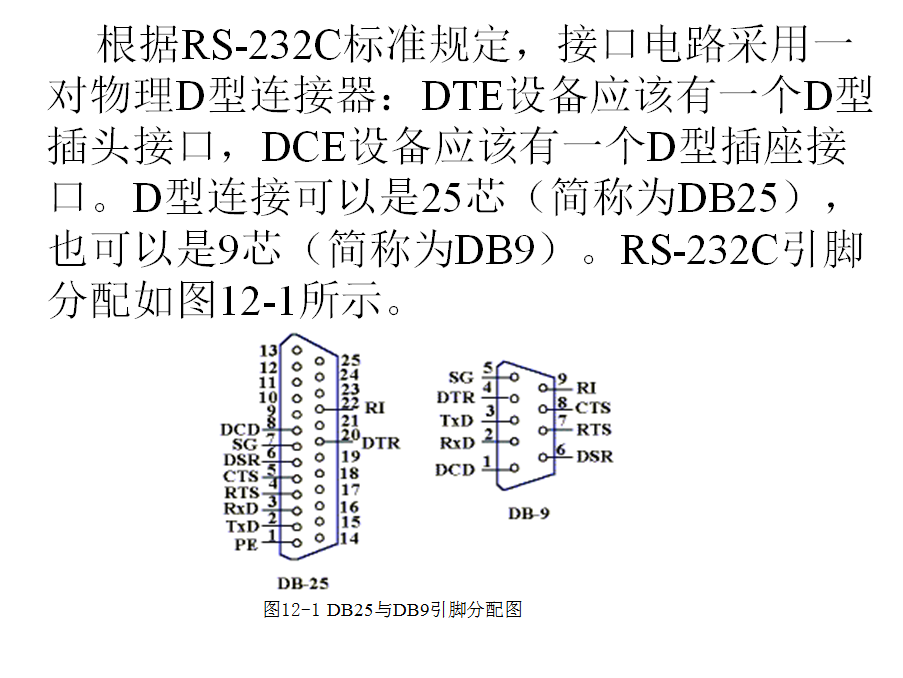
Delphi RS-232C标准的更多相关文章

  1. Delphi线程的终止

    当线程对象的Execute()执行完毕,我们就认为此线程终止了.这时候,它会调用Delphi的一个标准例程EndThread(),这个例程再调用API函数ExitThread().由ExitThrea ...

  2. Delphi颜色的表示（一共5种表示法）

    //全以红色举例: //1. RGB 模式:Self.Color := $0000ff; //不过和HTML.PhotoShop.FireWorks中的 #ff0000 是完全反的,应该叫 BGR. ...

  3. delphi 集合的用法

    http://blog.sina.com.cn/s/blog_9e2e8405010180jy.html delphi基础补充     1 开域语句     在面向对象的程序代码中,嵌套对象的现象十分 ...

  4. 【开发】MFC到Delphi的皮肤移植

       最近一直在学嵌入式,蛋疼啊,专业学软件的去搞硬件原理,真心有点伤不起,比较无聊,希望尽早脱离这个状态. 中午在林同学那里看到他在MFC上应用了Skin++皮肤,这是一款通用的软件换肤套件,支持各 ...

  5. HTML5, CSS3, ES5新的web标准和浏览器支持一览 转

    本文整理了一些最重要(或者说人气比较高罢)的新标准,虽然它们多数还只是w3c的草案,离Recommendation级别还早,却已经成为新一轮浏览器大战中备受追捧的明星,开发者社区里也涌现出大量相关的d ...

  6. 支付宝签名验证实现-Delphi版

    支付宝签名验证实现-Delphi版 首先介结下支付宝签名验证流程: 一  支付宝密钥生成 支付宝提供秘钥生成工具https://docs.open.alipay.com/291/105971/ 用此下 ...

  7. UART（串口）

    (1)串行通信线路三种工作方式:单工通信.半双工通信.全双工通信 单工:单工就是指A只能发信号,而B只能接收信号,通信是单向的. 半双工:半双工就是指A能发信号给B,B也能发信号给A,但这两个过程不能 ...

  8. stm32通信概述

    本文提到的内容有以下几个方面: 通信概述 串口通信 I2C通信 CAN通信 SPI通信 I2S通信 USB通信 其他通信 一.通信概述 按照数据传送方式分: 串行通信(一条数据线.适合远距离传输.控制 ...

  9. 浅谈对【OSI七层协议】的理解

    我们每天都在上网冲浪,在这背后到底有那些设备.协议去支撑呢?ISO是[Open System Interconnection]的缩写,该模型定义了不同计算机互联的标准,是设计和描述计算机网络通信的基本 ...

  10. stm32之通信

    本文提到的内容有以下几个方面: 通信概述 串口通信 I2C通信 CAN通信 SPI通信 I2S通信 USB通信 其他通信 一.通信概述 按照数据传送方式分: 串行通信(一条数据线.适合远距离传输.控制 ...

随机推荐

  1. ceph对接openstack环境（4）

    ceph对接openstack环境 环境准备: 保证openstack节点的hosts文件里有ceph集群的各个主机名,也要保证ceph集群节点有openstack节点的各个主机名 一.使用rbd方式 ...

  2. 基于scrapy框架的爬虫

    Scrapy是一个为了爬取网站数据,提取结构性数据而编写的应用框架. 可以应用在包括数据挖掘,信息处理或存储历史数据等一系列的程序中. scrapy 框架 高性能的网络请求 高性能的数据解析 高性能的 ...

  3. iOS创建带删除线和价钱符号的Label

    效果显示如下: 只需要子类化Label,重写DrawRect()方法即可: #import "MyLabel.h" @implementation MyLabel - (insta ...

  4. SQL SERVER CLR Trigger功能

    通过在 Microsoft SQL Server 中托管 CLR(称为 CLR 集成),开发人员可以在托管代码中编写存储过程.触发器.用户定义函数.用户定义类型和用户定义聚合函数, 改变了以前只能通过 ...

  5. Linux中权限控制ACL命令

    很多小伙伴觉得,Linux的权限管理命令不就是chown和chmod命令吗,什么时候有了ACL了? 什么是ACLACL是访问控制列表(Access Control List)的缩写,主要的目的是在提供 ...

  6. Python学习笔记——递归函数

    1.设置递归层数 #设置recursion函数的层数,默认是100层 import sys sys.setrecursionlimit(10000) 2. 阶乘 #定义一个阶乘函数 def facto ...

  7. beam search 和 greedy search

    贪心搜索(greedy search): 贪心搜索最为简单,直接选择每个输出的最大概率,直到出现终结符或最大句子长度. 集束搜索(beam search): 集束搜索可以认为是维特比算法的贪心形式,在 ...

  8. Android MVC MVP MVVM (一)

    示例效果 一共三个控件,EditText,Button,TextView 成功显示账号信息,查询失败显示错误信息. <?xml version="1.0" encoding= ...

  9. 吉首大学2019年程序设计竞赛（重现赛）- A SARS病毒 （矩阵，欧拉降幂）

    题目链接:https://ac.nowcoder.com/acm/contest/992/A 题意:求出长度为n的字符串个数,字符串由A.C.G.T组成,其中A和C必须成对出现. 思路:我们规定:   ...

  10. 阿里云服务器 lnmp安装流程

    nginx安装:wget http://nginx.org/download/nginx-1.12.2.tar.gztar zxvf nginx-1.12.2.tar.gzcd nginx-1.12. ...