BZOJ2616 SPOJ PERIODNI（笛卡尔树 + DP）

题意

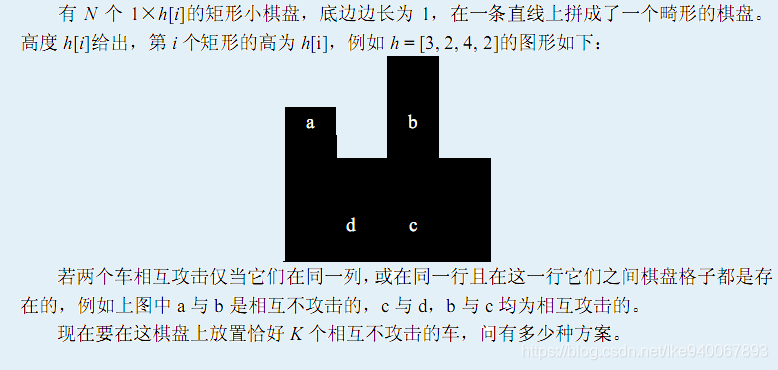
N,K≤500,h[i]≤106N,K\le 500,h[i]\le10^6N,K≤500,h[i]≤106

题解

建立出小根堆性质的笛卡尔树，于是每个节点可以代表一个矩形，其宽度为子树大小，高度为该节点记录的那一列高度-父节点那一列高度。

然后就可以随便DP了。

如果不会笛卡尔树，看看这张图，再看看代码就懂了（简单的笛卡尔树）。

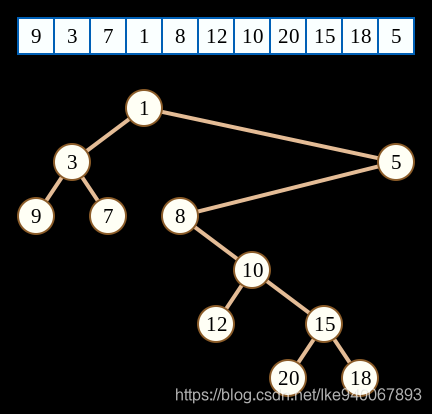
代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN = 505;
const int mod = 1e9 + 7;
const int MAXV = 1000005;
int n, k, rt, ch[MAXN][2], h[MAXN], tot, sz[MAXN];
int f[MAXN][MAXN], fac[MAXV], inv[MAXV];
inline int C(int N, int M) { return N < M ? 0 : 1ll * fac[N] * inv[M] % mod * inv[N-M] % mod; }
void ins(int &x, int v) {
	if(!x) { h[x = ++tot] = v, sz[x] = 1; return; }
	if(v >= h[x]) ins(ch[x][1], v);
	else ch[++tot][0] = x, x = tot, h[tot] = v;
	sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + 1;
}
void dfs(int x, int ff) {
	if(ch[x][0]) dfs(ch[x][0], x);
	if(ch[x][1]) dfs(ch[x][1], x);
	for(int i = 0; i <= sz[ch[x][0]]; ++i)
		for(int j = 0; j <= sz[ch[x][1]]; ++j)
			f[x][i+j] = (f[x][i+j] + 1ll * f[ch[x][0]][i] * f[ch[x][1]][j] % mod) % mod;
	for(int i = sz[x]; i >= 0; --i)
		for(int j = 1; j <= i && j <= h[x]-h[ff]; ++j)
			f[x][i] = (f[x][i] + 1ll * f[x][i-j] * C(h[x]-h[ff], j) % mod * C(sz[x]-(i-j), j) % mod * fac[j] % mod) % mod;
}
int main () {
	fac[0] = fac[1] = inv[0] = inv[1] = 1;
	for(int i = 2; i < MAXV; ++i) inv[i] = 1ll * (mod - mod/i) * inv[mod%i] % mod;
	for(int i = 2; i < MAXV; ++i) fac[i] = 1ll * fac[i-1] * i % mod, inv[i] = 1ll * inv[i] * inv[i-1] % mod;
	scanf("%d%d", &n, &k);
	for(int i = 1, x; i <= n; ++i) scanf("%d", &x), ins(rt, x);
	f[0][0] = 1;
	dfs(rt, 0);
	printf("%d\n", f[rt][k]);
}