Can you answer these queries III

Can you answer these queries III

题目:洛谷　　SPOJ

【题目描述】

给定长度为N的数列A，以及M条指令，每条指令可能是以下两种之一：

1.“0 x y”，把A[x]改成y；

2.“1 x y”，查询区间[x,y]中的最大连续子段和。

【输入格式】

第一行，N；

第二行，N个数，即A[1]...A[N]；

第三行，M；

第4至第M+3行，每行三个整数，分别表示“0或1”，x，y，即指令。

【输出格式】

i行，i表示“1 x y”的数量，每行1个整数，即指令2的答案。

【数据规模】

N,M<=50000。

解析

查询区间最大连续子段和，显然可以用线段树维护序列。

先分析一下，在线段树中，对于查询的每个区间[x,y]，会有以下两种情况：

1、如图所示，区间刚好在一个子树中，只需查询该子树的区间最大连续子段和即可；

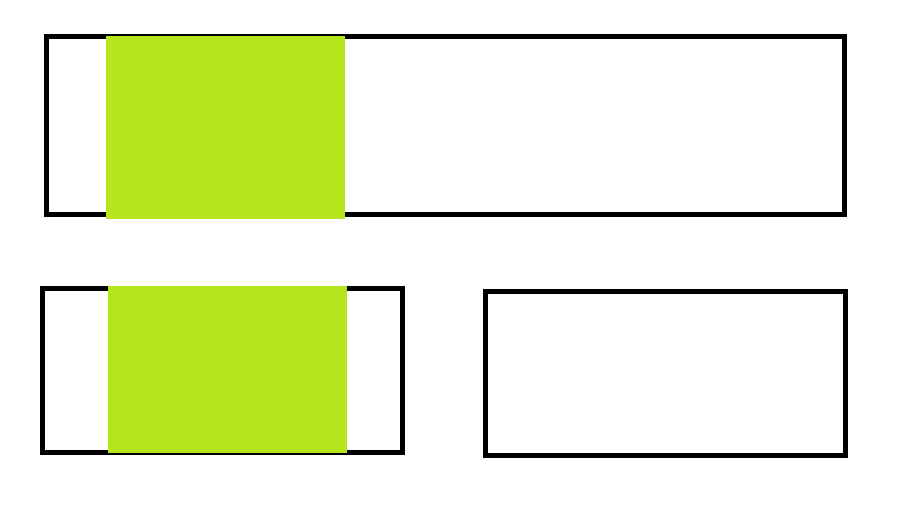
2、如图所示，区间一部分在左子树中，另一部分在右子树中，对于这种情况，该区间的最大连续子段和为左子树的最大后缀和加上右子树的最大前缀和。

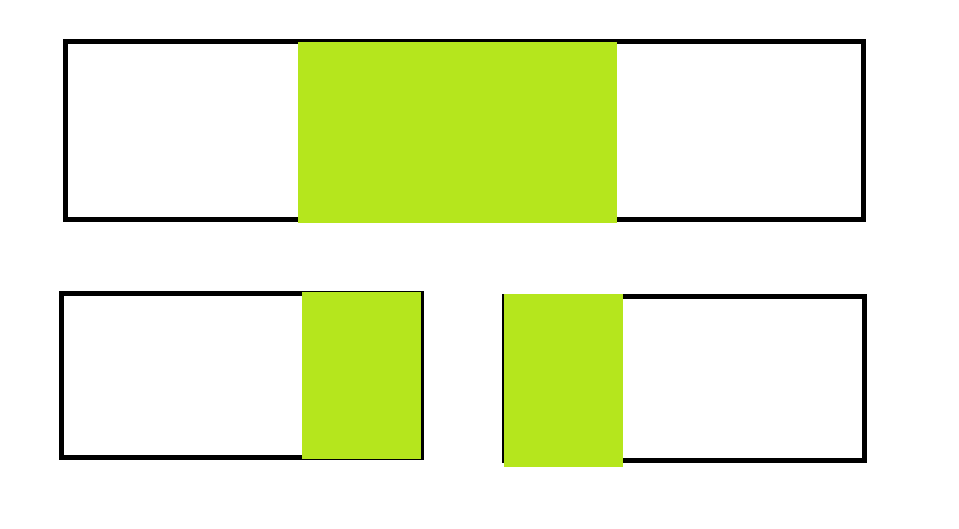
考虑完所有情况后，只需套上线段树模板再稍作修改即可。

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;
struct rec{
    int l,r,maxn,lmax,rmax,sum;//lmax最大前缀和,rmax最大后缀和
}t[];
int n,m,a[];
void build(int p,int l,int r)
{
    t[p].l=l,t[p].r=r;
    if(l==r)
    {
        t[p].sum=t[p].lmax=t[p].rmax=t[p].maxn=a[l];
        return ;
    }
    int mid=(l+r)/;
    build(p*,l,mid);
    build(p*+,mid+,r);
    t[p].sum=t[p*].sum+t[p*+].sum;
    t[p].lmax=max(t[p*].lmax,t[p*].sum+t[p*+].lmax);
    t[p].rmax=max(t[p*+].rmax,t[p*+].sum+t[p*].rmax);
    t[p].maxn=max(t[p*].rmax+t[p*+].lmax,max(t[p*].maxn,t[p*+].maxn));
    return ;
}
void change(int p,int x,int v)
{
    if(t[p].l==t[p].r)
    {
        t[p].sum=t[p].rmax=t[p].lmax=t[p].maxn=v;
        return ;
    }
    int mid=(t[p].l+t[p].r)/;
    if(x<=mid) change(p*,x,v);
    else change(p*+,x,v);
    t[p].sum=t[p*].sum+t[p*+].sum;
    t[p].lmax=max(t[p*].lmax,t[p*].sum+t[p*+].lmax);
    t[p].rmax=max(t[p*+].rmax,t[p*+].sum+t[p*].rmax);
    t[p].maxn=max(t[p*].rmax+t[p*+].lmax,max(t[p*].maxn,t[p*+].maxn));
}
rec ask(int p,int l,int r)
{
    if(l<=t[p].l&&r>=t[p].r) return t[p];
    rec a,b,ans;
    a.sum=a.lmax=a.rmax=a.maxn=b.sum=b.lmax=b.rmax=b.maxn=0xcfcfcfcf;
    ans.sum=;
    int mid=(t[p].l+t[p].r)/;
    if(l<=mid)
    {
        a=ask(p*,l,r);
        ans.sum+=a.sum;
    }
    if(r>mid)
    {
        b=ask(p*+,l,r);
        ans.sum+=b.sum;
    }
    ans.maxn=max(max(a.maxn,b.maxn),a.rmax+b.lmax);        //注意负数
    ans.lmax=max(a.lmax,a.sum+b.lmax);
    ans.rmax=max(b.rmax,b.sum+a.rmax);
    if(l>mid) ans.lmax=max(ans.lmax,b.lmax);
    if(r<=mid) ans.rmax=max(ans.rmax,a.rmax);
    //分类讨论
    return ans;
}
int main()
{
    int c,l,r;
    cin>>n;
    for(int i=;i<=n;i++) cin>>a[i];
    build(,,n);
    cin>>m;
    for(int i=;i<=m;i++)
    {
        cin>>c>>l>>r;
        if(c==) change(,l,r);
        else cout<<ask(,l,r).maxn<<endl;
    }
    return ;
}