【ZJOI 2016】旅行者

题意

　　http://uoj.ac/problem/184

题解

　　大概是神题。

　　网格图上跑最短路有一个经典的优化方式：分治分组跑最短路。
　　对于这道题，设矩形长为 \(n\)，宽为 \(m\)，则对 \(n,m\) 中更大的一个二分。
　　这里只考虑按 \(n\) 分治的情况。

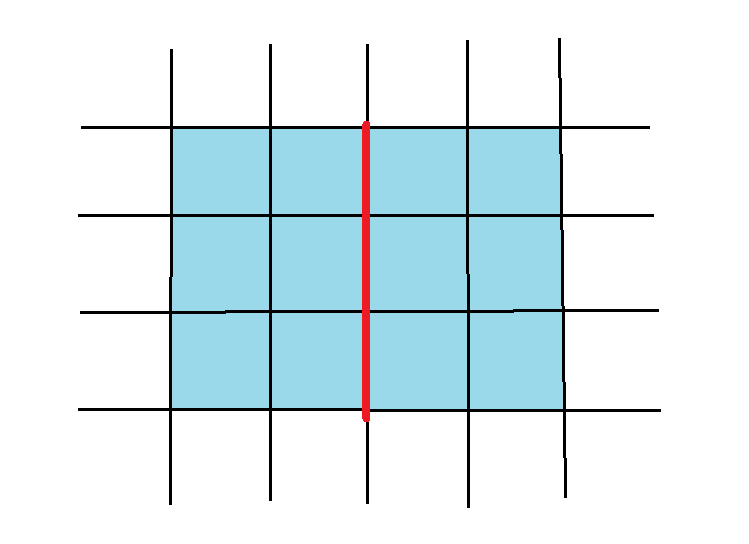
　　如上图，设 \(S=nm\)，因为此时一列的点数是小等于 \(\sqrt{S}\) 的，所以我们可以枚举红色分割线上的点，以每个点为原点，跑到矩形中所有点的最短路。
　　然后考虑询问：
　　　　如果询问的两点在分割线的不同侧（或者至少有一端在分割线上），则最短路一定经过分割线，用分割线上的每个点到这两个点的最短距离之和更新答案，然后这个询问就不用管了。
　　　　如果询问的两点在分割线的同一侧，则最短路可能经过分割线，依然用分割线上的每个点到这两个点的最短距离之和更新答案，然后把这个询问扔到左/右递归区间，去寻找不经过分割线的最短路。
　　　　当然，有可能存在分割线上一点 到询问两端的最短路存在部分重合的情况。对于不同侧的情况，画图可知这种情况会被分割线上其它点 用更短路径覆盖掉；对于同一侧的情况，这种情况会被不经过分割线的更短路径覆盖掉。

　　时间复杂度 \(O(S\sqrt{S}\log^2{S})\)。嗯，码吧……
　　……
　　等等，你他吗说什么？这复杂度什么破玩意？？跟 \(O(S^2)\) 有啥区别？？你让我 \(2s\) 跑带大常数的 \(4e8\)？？?如果 cpu 是 I9 的说不定真能跑过
　　其实刚才这个复杂度是凭感觉意淫的，下面就是丧心病狂的算时间复杂度环节了

　　首先有 \[\begin{align} T(S)&=2T(\frac{S}{2})+O(S\sqrt{S}\log S) \nonumber \\ &= T(S)=2T(\frac{S}{2})+O(S^{1.5}\log S) \nonumber \end{align}\]
　　然后参考这篇博客的主定理（这里有简单版）
　　假设我们有递归式 \(T(n)=aT(\frac{n}{b})+f(n)\)，我们可以用主定理解这个递归式。
　　其中 \(n\) 为问题的规模，\(a\) 为递归到下一层的子问题数量，\(\frac{n}{b}\) 为每个子问题的规模，\(f(n)\) 为递推后做的额外计算。
　　本题中，\(a=b=2\)，\(f(S)=O(S^{1.5}\log S)\)。

• 1. 假设存在常数 \(\epsilon>0\)，使得 \(f(n)=O(n^{\log_b(a)-\epsilon})\)，则 \(T(n)=\Theta(n^{log_ba})\)
  　　\(\log_b a = \log_2 2 = 1\)，则 \(S^{1-\epsilon}=S^{1.5}\log S\)，显然 \(\epsilon<0\)，故不符合主定理 1。

• 2. 假设存在常数 \(k\ge 0\)，使得 \(f(n)=\Theta (n^{\log _{b}a}\log ^{k}n)\)，则 \(T(n)=\Theta(n^{log_ba}\log^{k+1}n)\)。
  　　\(S^{\log_b a}\log^k S = S\log^k S = S^{1.5}\log S\)
  　　即要求 \(log^{k-1} S = S^{0.5}\)
  　　参考具体数学第2版 p368 的渐进等级次序，可知 \(\log_x n\lt n^c\)，其中 \(x\) 是任意 \(\gt 1\) 的底数，\(c\) 是任意 \(\gt 1\) 的指数，\(<\) 号重定义为函数的渐进增长率关系，即右边的函数更快到达无穷大。
  　　比如有 \(\log n\lt n^{0.0001}\)，这可能是很多人都不敢相信的，因为我们通常将视野局限于 \(n\) 不够大的情况，这种情况下 \(\log n\) 的值当然远大于 \(n^{0.0001}\)。比如 \(n=10^{100}\)，\(\log n=100\)，\(n^{0.0001}≈1.0233\)。但如果我们把 \(n\) 取到 \(10^{10^{100}}\)，\(\log n\) 就小于 \(n^{0.0001}\) 了。
  　　那把 \(\log_x n\) 取任意实数次幂，其增长速度是否还小于 \(n^c\) 呢？
  　　确实是的。我们观察渐进增长率关系的定义：\[ f(n)<g(n) \rightleftharpoons \lim_{n \to \infty} \frac{f(n)}{g(n)}=0\]
  　　显然对于任意实数 \(y\)，都有 \(\frac{f(n)^y}{g(n)}=0\)。故二者的渐进增长率关系不变。
  　　（这其实算是高数内容了，有点超纲，了解一下就好）
  　　综上，\(log^{k-1} S = S^{0.5}\) 是不可能满足的，随着 \(S\) 的增长，二者的趋向无穷大的速度一定不同，只要 \(S\) 取得足够大，二者的取值就会不同。
  　　故不符合主定理 2。

• 3. 假设存在常数 \(\epsilon >0\)，有 \(f(n)=\Omega (n^{\log _{b}(a)+\epsilon })\)，同时存在常数 \(c<1\) 以及充分大的 \(n\) 满足 \(af(\frac{n}{b})\le cf(n)\)，那么 \(T\left(n\right)=\Theta \left(f\left(n\right)\right)\)。
  　　其实前两个主定理都不符合了，那肯定是用主定理 3 算复杂度了……
  　　本来想验证一下是否满足主定理 3 的，结果主定理 3 的那个 \(\Omega\) 我不会解啊 QvQ，哪位哥哥教教我

　　于是套用主定理 3，算得 \(T\left(n\right) = \Theta \left(f\left(n\right)\right) = \Theta (S\sqrt{S}\log S)\)。
　　所以时间复杂度是 \(\Theta (S\sqrt{S}\log S)\)（带不及 \(\log S\) 的小常数）……

　　这题有一个弱化版，就是强制 \(n\le 10^5\)，\(m\le 10\)，这时由于递归式里不带 \(\sqrt{S}\)，要套主定理 2 而不是主定理 3，所以解出来的时间复杂度是 \(\Theta (mS\log m\log {S})\)。这就是双 \(\log\) 复杂度说法的来源……

　　code