R树-javascript代码实现过程分析（插入操作）

R Tree

第一步，创建R树类。

构建一个RTree生成器。用以创建tree对象。

例子：var tree = new RTree(12)

var RTree = function(width){
  var _Min_Width = 3;  // Minimum width of any node before a merge
    var _Max_Width = 6;  // Maximum width of any node before a split
    if(!isNaN(width)){ _Min_Width = Math.floor(width/2.0); _Max_Width = width;}
    // Start with an empty root-tree
    var _T = {x:0, y:0, w:0, h:0, id:"root", nodes:[] };
 
    var isArray = function(o) {
        return Object.prototype.toString.call(o) === '[object Array]';
    };
 
  var _attach_data = function(node, more_tree){
        node.nodes = more_tree.nodes;
        node.x = more_tree.x; node.y = more_tree.y;
        node.w = more_tree.w; node.h = more_tree.h;
        return(node);
    };
 
  //选择适合的节点来存放插入的条目。
  //@private。
  var _choose_leaf_subtree = (rect, root) => {...}
 
  //内部插入函数。
  //[] = _insert_subtree(rectangle, object to insert, root to begin insertion at)
  //@private。即私有函数，只能用RTree的方法调用它。
  var _insert_subtree = (node, root) => {...}
 
  this.get_tree = function() { return _T}
 
  //new_tree代表新的子树节点，where代表要替代的位置。
  this.set_tree = (new_tree, where) => {
    if (!where) {
          where = _T
        }
    return (_attach_data(where, new_tree))
  }
 
  //rect是边界矩阵，对象是叶子节点。
  this.insert = (rect, obj) => {
    if (arguments.length < 2) {
          throw "Wrong number of arguments"
        }
    return (_insert_subtree({x:rect.x, y:rect.y, w:rect.w, h:rect.h, leaf:obj}, _T))
  }
 
// End of RTree
}

tree.insert方法，用以向生成的R树，插入数据。方法见下：

把一个新的索引条目E插入一个R树内：

1. 找到插入新记录的位置： 这里要调用Choose Leaf方法，选择一个叶节点L来存放E。

把记录E加入到叶节点中： 这里需要进行判断。

• 如果L.nodes <= M（即L的条目数量此时小于等于规定的最大值M），则下一步;
• 否则, 需要分裂，调用Split Node方法。把叶子节点L分裂成2个新节点L和LL（2个新节点包含了原来的L节点的所有条目和新条目E）。
2. 向上传递变化：调用Adjust Tree方法对L节点操作。如果上一步是分裂操作，则对2个新节点调用Adjust Tree方法。
3. 判断：是否树增高。如果节点的分裂导致了root的分裂，则需要生成新的root,并且让它的两个孩子节点为原来的root分裂后产生的2个节点。

第二步：生成R树。

var tree = new RTree(12)、
tree.insert(rect, obj)

调用tree.insert(rect, obj)方法, 向R树插入数据，参数有2个，rect是边界矩阵对象，obj是节点对象。

由此，引入rectangle的构建器。

//Rectangle - 生成rectangle对象。
RTree.Rectangle = function(ix, iy, iw, ih) {
  var x, x2, y, y2, w, h;
 
  if(ix.x) {
    x = ix.x;y = ix.y; //得到左下角坐标
 
    if(ix.w !== 0 && !ix.w && ix.x2){
      //如果长，宽不存在，则计算出来。
      w = ix.x2-ix.x;    h = ix.y2-ix.y;
    }    else {
      w = ix.w;    h = ix.h;
    }
 
        x2 = x + w; y2 = y + h; //得到第右上角的坐标
    } else {
        x = ix; y = iy;    //得到左下角坐标
    w = iw;    h = ih;
        x2 = x + w; y2 = y + h;  //得到第右上角的坐标
    }
 
  this.x1 = this.x = x;
  this.y1 = this.y = y;
  this.x2 = x2;
  this.y2 = y2;
  this.w =  w;
  this.h =  h;
 
  //矩阵a和当前矩阵产生部分重合则，返回true。
  this.overlap = (a) => {...}
  //扩展当前矩阵。根据传入的矩阵a,来扩展，包含矩阵a.
  this.expand = (a) => {...}
  //重置当前矩阵的坐标和长宽。代码同初始化Rectangle的代码。
  this.setRect = (ix, iy, iw ,ih) {...}
// End of Rectangle
}

overlap方法的解释（代码）：

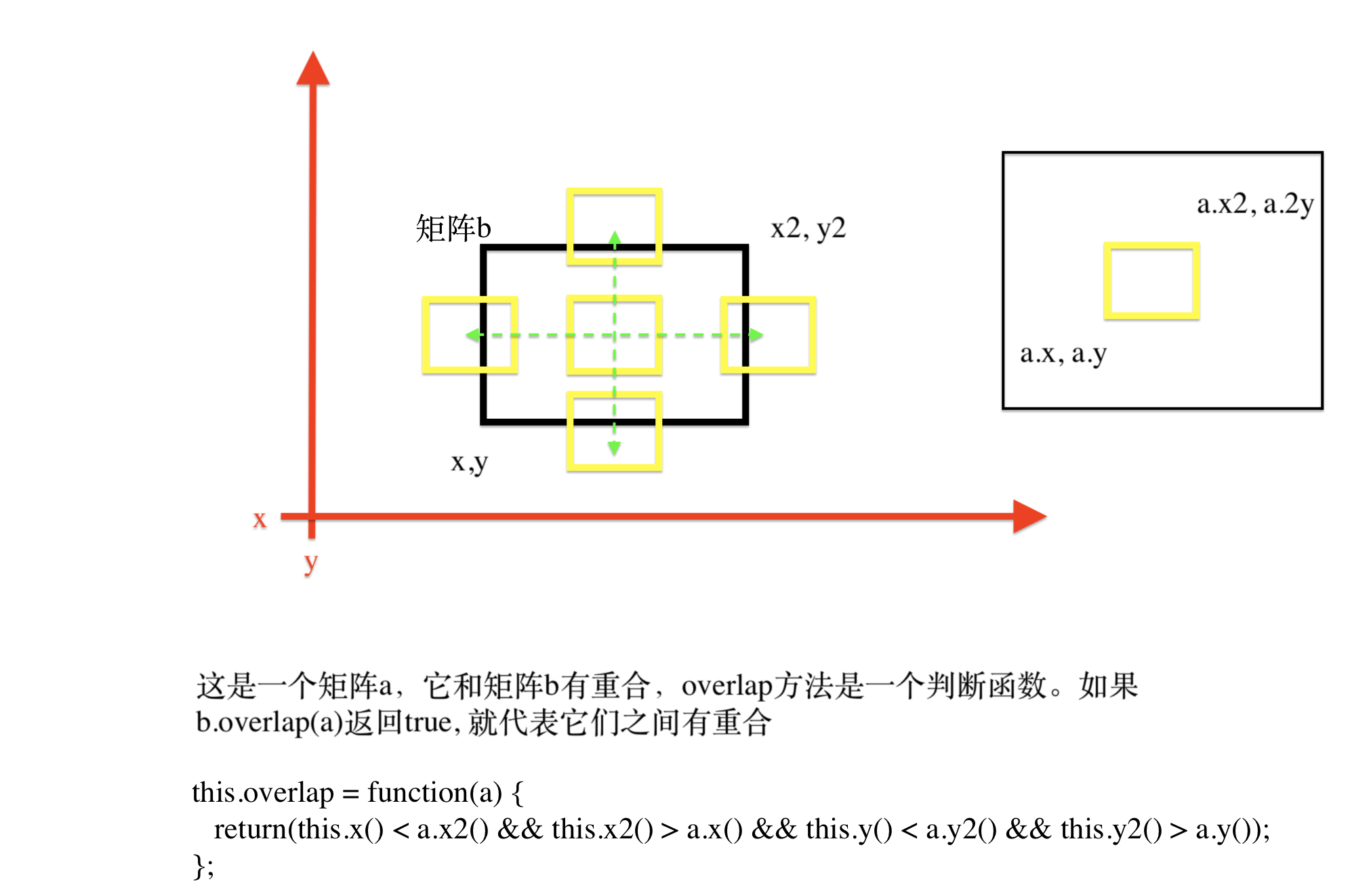
expand方法的解释：

插入一个矩阵，到叶子节点，对应的父亲的最小边界矩阵由此可能要扩展。矩阵b要把插入的a的矩阵包含进自己。

    this.expand = function(a) {
        var nx = Math.min(this.x(), a.x());
        var ny = Math.min(this.y(), a.y());
        w = Math.max(this.x2(), a.x2()) - nx;
        h = Math.max(this.y2(), a.y2()) - ny;
        x = nx; y = ny;
        return(this);
    };

第三步：插入方法讲解

这里要调用插入方法。

//得到一个最小边界矩阵。
var rect = new RTree.Rectangle(2,2,3,3)

var tree = new RTree(12)
tree.insert(rect, obj)

在插入一个rect后，为了要把rect放到正确的叶节点中。首先要找到这个叶节点，需要调用choose leaf方法。

//在insert方法内的_insert方法内调用
 var tree_stack = _choose_leaf_subtree(node, root) //node参数就是最开始传入insert()的第一个参数

方法_choose_leaf_subtree:

  //选择适合的节点来存放插入的条目。
  //从root节点开始一路向下，每次找到当前节点的条目中，那个被插入新矩阵后，需要扩展最小的条目。就是被选择的条目。
  //直到到达叶子节点。最后返回：从root节点到叶子节点，经过的节点的集合数组。
  var _choose_leaf_subtree = (rect, root) => {
    var best_choice_index = -1;  //记录最合适的节点索引，并用它来控制do..while循环
    var best_choice_stack = [];  //方法结束后，返回从root节点到叶子节点，经过的节点的集合数组。
    var best_choice_area;        //用于比较扩展的区域大小。
 
    best_choice_stack.push(root); //返回的变量的第一个元素是root。
    var nodes = root.nodes;    //首先，变量nodes记录根节点的所有的条目，用于循环代码。
 
    do {
      if(best_choice_index != -1){
        best_choice_stack.push(nodes[best_choice_index]); //储存当前最合适的条目。
        nodes = nodes[best_choice_index].nodes;  //修改nodes，为被选中的条目的nodes集合。其实就是准备下一层的条目的判断。
        best_choice_index = -1;
      }
 
      //第一次循环，遍历root的所有项目。
      //变量：当前节点的所有条目/项目。找到添加rect后，扩展最小的那个条目。
      //当i等于-1，当前节点的所有条目的判断结束，
      for(var i = nodes.length-1; i >= 0; i--) {
        var ltree = nodes[i];
 
        //如果到达叶节点，结束for循环。leaf是hash对象的索引，由_insert_subtree传入。
        if("leaf" in ltree) {
          best_choice_index = -1; //通过变量，同时也保证会退出do..while循环。
          break;
        }
        //下面的代码用于计算当前条目被插入新矩阵后，扩展的面积。然后用best_choice_area记录最小的扩张面积。
        //这里使用一种特殊的算法。
        //原矩阵正方化。一种算法。
        var old_lratio = RTree.Rectangle.squarified_ratio(ltree.w, ltree.h, ltree.nodes.length+1);
 
        // 扩展矩阵。
        var nw = Math.max(ltree.x+ltree.w, rect.x+rect.w) - Math.min(ltree.x, rect.x);
        var nh = Math.max(ltree.y+ltree.h, rect.y+rect.h) - Math.min(ltree.y, rect.y);
 
        // 新扩展的矩阵的正方化。
        var lratio = RTree.Rectangle.squarified_ratio(nw, nh, ltree.nodes.length+2);
 
        //扩展的面积的比较，我们需要用变量记录最小扩展面积。
        if(best_choice_index < 0 || Math.abs(lratio - old_lratio) < best_choice_area) {
          best_choice_area = Math.abs(lratio - old_lratio);
          best_choice_index = i;
        }
      }
    } while(best_choice_index != -1)
 
    return(best_choice_stack)
  }

找到要插入的位置后，进行第2步判断是否需要分裂节点。

再然后进行第3步，向上调整边界矩阵。

• 这时要判断第二步是否有分裂节点的情况。如果是，那么对分裂出来的2个新节点的矩阵都要进行性调整。即调用RTree.Rectangle.expand_rectangle方法。
• 如果false。就对原来的节点调整。

最后一路到达根节点，同样对根节点进行第2步的判断，第3步的调整，最后完成插入操作。

看_insert_subtree

  //[] = _insert_subtree(rectangle, object to insert, root to begin insertion at)
  //@private。即私有函数，只能用RTree的方法调用它。
  var _insert_subtree = (node, root) => {
    var bc //Best current node
 
    // 初始化插入。如果根节点还没有儿子，那么这个节点的最小边界矩阵，就是root节点的MBR。
    if (root.nodes.length == 0) {
      root.x = node.x; root.y = node.y;
      root.w = node.w; root.h = node.h;
      root.nodes.push(node);
      return;
    }
 
    //找到最适合的叶子节点来插入条目
    var tree_stack = _choose_leaf_subtree(node, root) //return得到从root到叶子，经过的所有节点的集合。
    var ret_obj = node //{x: rect.x, y:rect.y, w:rect.w, h:rect.h, leaf:obj}, 这个变量代表循环内要调整的条目。
 
    //向上传递变化。包括插入的第2-4步骤，对tree_stack增减其中的元素，控制循环次数。
    do {
      //第一次循环会调用else块的语句，bc被赋值为叶节点对象, 同时tree_stack也发生变化，用于控制循环。
            if(bc && "nodes" in bc && bc.nodes.length == 0) {  //handle the case of an empty node (from a split) 。 删除空节点。
                var pbc = bc; // Past bc
                bc = tree_stack.pop();
                for(var t=0; t<bc.nodes.length; t++)  　　　　//for循环没有带{}，⚠️这种写法
                  if(bc.nodes[t] === pbc || bc.nodes[t].nodes.length == 0) {
                      bc.nodes.splice(t, 1);  //删除这个条目。
                      break;
                　}
            } else {
                bc = tree_stack.pop();
            }
 
      // If there is data attached to this ret_obj，
      // 如果rec_obj对象含有属性"leaf",或"nodes",或一个数组（内含多2个新节点/条目）
            if("leaf" in ret_obj || "nodes" in ret_obj || isArray(ret_obj)) {
                // 调整和插入。
                if(isArray(ret_obj)) {  //如果上一轮循环是分裂情况，那么需要把分裂的节点放入父亲点，并调整矩阵。
                    for(var ai = 0; ai < ret_obj.length; ai++) {      //让bc扩展到可以包含所有ret_obj内的条目。
                        RTree.Rectangle.expand_rectangle(bc, ret_obj[ai]);
                    }
                    bc.nodes = bc.nodes.concat(ret_obj);              //叶节点bc的条目增加
                } else { //正常情况，也是调整矩阵，然后插入。
                    RTree.Rectangle.expand_rectangle(bc, ret_obj);
                    bc.nodes.push(ret_obj); // 插入一个条目到节点bc。
                }
 
        　　　　  //当插入完成后，第二步判断bc的条目是否超出最大值限制。
       　　　　　 // true: rec_obj被重新赋值，因为没有"leaf",'nodes'属性，后续轮循环代表一路向上调整最小限定矩阵。
       　　　　　 // false: 则需要分裂。然后也要对分裂后的节点进行调整。
                if(bc.nodes.length <= _Max_Width)    {
                    ret_obj = {x:bc.x,y:bc.y,w:bc.w,h:bc.h};  //后续循环只需调整MBR。
                }    else { // 否则，要分裂
                    // 调用linear_split()，返回包括2个新节点的数组。
                    // formed from the split of the previous node's overflow
                    var a = _linear_split(bc.nodes);
                    ret_obj = a;  //这时ret_obj是一个数组。
 
                    if(tree_stack.length < 1)    { // 如果正在分裂root节点， tree_stack已经为空。这是插入操作的第4步。
                        bc.nodes.push(a[0]);
                        tree_stack.push(bc);     //重新考虑root元素。
                        ret_obj = a[1];
                    } /*else {
                        delete bc;
                    }*/
                }
            } else {
        　　 　//插入操作第3步骤。
        　　　 //如果不是上面的情况：rect_obj只是一个含有矩阵信息的对象。就只更新bc的最小限定矩阵。
              RTree.Rectangle.expand_rectangle(bc, ret_obj);
              ret_obj = {x:bc.x,y:bc.y,w:bc.w,h:bc.h};
            }
    }while(tree_stack.length > 0)
  }

根据插入操作的流程，可理解代码。这里还没有讲解分裂方法：_linear_split()。

为了优化R树，大神们开发了多种分裂算法。这里使用的是linear split。

具体看 Hilbert R树发展 这篇文章讲解了分裂算法的发展历史。

⚠️R*树的方法是对R树最好的优化。

分裂算法也是很复杂的。没有仔细理解这个分裂算法。

    //split方法：分裂一个节点的条目，把它们放到2个新的节点中。⚠️分裂方法不同，放置也不同。这里使用linear split。
    // [ an array of two new arrays of nodes ] = linear_split(array of nodes)
    // @private
    var _linear_split = function(nodes) {
        var n = _pick_linear(nodes);
        while(nodes.length > 0)    {
            _pick_next(nodes, n[0], n[1]);
        }
        return(n);
    };

里面的私有方法：

1. pcik_linear返回数组，把原来数组内的条目，分成2组。每组的条目属于一个新的节点。
2. pick_next则是把最好的MBR插入到节点a, b。

具体代码见：https://github.com/imbcmdth/RTree/blob/master/src/rtree.js

关于插入操作就讲解完了。