关于cubic-bezier 贝塞尔曲线的简单了解
在animation和transition两个属性中，cubic-bezier是控制变化的速度曲线，主要是生成速度曲线的函数
规定用法是： cubic-bezier(<x1>,<y1>,<x2>,<y2>)
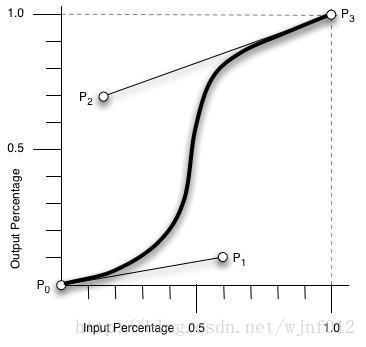
从上图中可以看到，cubic-bezier有四个点：
两个默认的，即：P0(0,0)，P3(1,1)；
两个控制点，即：P1(x1,y1)，P2(x2,y2) （这是我们设置的两个点）
注：X轴的范围是0~1，超出cubic-bezier将失效，Y轴的取值没有规定，但是也不宜过大。
我们只要调整两个控制点P1和P2的坐标，最后形成的曲线就是动画曲线。
关于cubic-bezier 贝塞尔曲线的简单了解的更多相关文章
- cocos2d-x 贝塞尔曲线的简单运用（CCBezierTo，CCBezierBy）
原文链接:http://blog.csdn.net/we000636/article/details/8616355 一.贝赛尔曲线简单介绍 贝塞尔曲线是应用于二维图形应用程序的数学曲线.曲线的定义有 ...
- 贝塞尔曲线UIBezierPath简单使用
//常用属性 /* 1.CGPath: 将UIBezierPath类转换成CGPath 2.currentPoint: 当前path的位置,可以理解为path的终点 3.lineWidth: 线条宽度 ...
- Bezier贝塞尔曲线的原理、二次贝塞尔曲线的实现
Bezier曲线的原理 Bezier曲线是应用于二维图形的曲线.曲线由顶点和控制点组成,通过改变控制点坐标可以改变曲线的形状. 一次Bezier曲线公式: 一次Bezier曲线是由P0至P1的连续点, ...
- 关于photoshop钢笔工具中各点对应到“贝塞尔曲线”中的含义（cocos2d-x与iOS）
1.程序中贝塞尔曲线的简单介绍,只介绍曲线部分.程序中的贝塞尔曲线需要四个点:起始点(startPoint) ,控制点1(controlPoint1),控制点2(controlPoint2),结束点( ...
- 你知道吗， CoreGraphics绘图系统和Bezier贝塞尔曲线坐标系的顺时针方向是相反的！
UIBezierPath是对Core Graphics框架的一种上层封装,目的是让绘图需求可以被更方便的使用. 那你有没有发现被UIBezierPath封装后与之前有什么改变? 答:有三个变化. 1. ...
- 贝塞尔曲线（cubic bezier）
对于css3的Transitions,网上很多介绍,相信大家都比较了解,这里用最简单的方式介绍下: transition语法:transition:<transition-property> ...
- Android -- 贝塞尔曲线公式的推导和简单使用
1,最近看了几个不错的自定义view,发现里面都会涉及到贝塞尔曲线知识,深刻的了解到贝塞尔曲线是进阶自定义view的一座大山,so,今天先和大家来了解了解. 2,贝塞尔曲线作用十分广泛,简单举几个的栗 ...
- 贝塞尔（Bezier） 曲线 研究
贝塞尔曲线最近经常接触到,今天研究了一下. 原理 关于它的原理,网上有很多. 1.一阶 2.二阶 3.多阶 可以看到,多阶可以慢慢降阶为一阶贝塞尔曲线. //一阶 private Vector3 Ba ...
- 贝塞尔曲线.简单推导与用opengl实现动态画出。
在opengl中,我们可以用少许的参数来描述一个曲线,其中贝塞尔曲线算是一种很常见的曲线控制方法,我们先来看维基百科里对贝塞尔曲线的说明: 线性贝塞尔曲线 给定点P0.P1,线性贝塞尔曲线只是一条两点 ...
随机推荐
- Jupyter Notebook 远程连接配置（转载）
转载博客的Jupyter Notebook远程连接配置方法. 0 - 参考资料 https://www.jianshu.com/p/08f276d48669?utm_campaign=maleskin ...
- osg fbx 模型结构操作
osg::Node* TeslaManage::findOsgNodeByName(QString &nodeNme) { osg::Node* findNode = NULL; std::v ...
- php上传超大文件
1.使用PHP的创始人 Rasmus Lerdorf 写的APC扩展模块来实现(http://pecl.php.net/package/apc) APC实现方法: 安装APC,参照官方文档安装,可以使 ...
- （四）java对象的结构和对象的访问定位
在HotSpot虚拟机中,对象在内存中存储的布局可以分为3块区域:对象头(Header).实例数据(Instance Data)和对齐填充(Padding). 一. 对象头 HotSpot虚拟机的对象 ...
- activity 工作流
https://blog.csdn.net/cs_hnu_scw/article/details/79059965 https://blog.csdn.net/xnf1991/article/deta ...
- python登录项目
简单的django登录项目 1.首先建立工程,建立工程请参照:https://www.cnblogs.com/effortsing/p/10394511.html 2.在Firstdjango工程项目 ...
- python配置yum源
import subprocess import sys import os def main(): try: subprocess.call(["yum install wget -y;c ...
- IE和火狐的css兼容性问题
CSS对浏览器器的兼容性具有很高的价值,通常情况下IE和Firefox存在很大的解析差异,这里介绍一下兼容要点. 1.DOCTYPE 影响 CSS 处理 2.FF: div 设置 margin-le ...
- linux系统时间设定
更改系统时间并同步硬件时钟 sudo date -s '2018-12-27 12:46' sudo hwclock --systohc hwclock说明:hwclock --help
- Caché到MySQL数据同步方法!
随着医疗行业信息化的发展,积累了大量的业务数据,如何挖掘这些数据,实现数据的可视化被提上日程,医院中通常有许多的信息化系统,使用的又都是不同厂商的数据库产品,如何统一汇聚数据,实现数据互通也是一个大问 ...