LESSON 6- Quantization

如果输入本身就是离散的（比如text, computer files…）, 对于这种discrete sources不需要量化可以直接进行离散信源编码。

如果输入是waveform（比如声音），取样为模拟信号，那么在进行离散编码前需要进行量化，将模拟信号转为数字信号。

If input is discrete (such as text, computer files...), then there is no need quantizing such discrete sources. If the input is waveforms (such as sound) and is sampled as an analog signal, then quantization is required to convert the analog signal to a digital signal before discrete encoding.

1.      量化所在层级(Quantization’s layer):

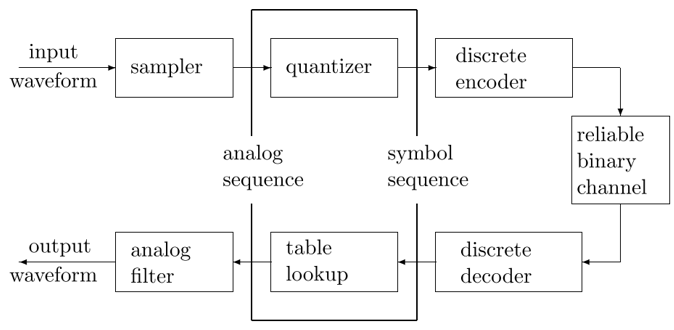
2.      量化具体步骤(Quantization procedures)：

3.      非均匀量化(Non-uniform quantization）

1)       为什么语音信号必须使用非均匀量化

When processing speech signals, why do we have to use non-uniform quantization not uniform quantization.

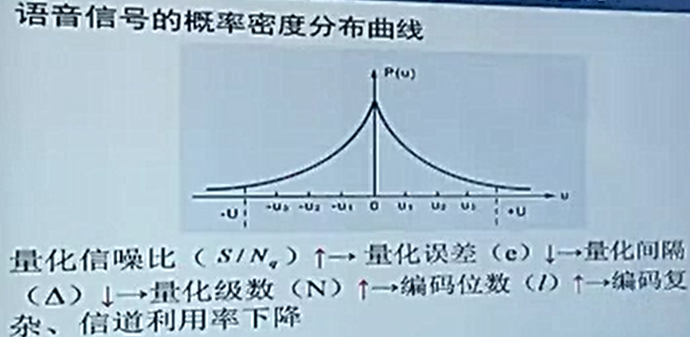
语音信号的概率分布服从指数分布，小信号占比多。要想提高量化信噪比，降低量化误差，需要增加量化级数，这会导致编码复杂。

The speech signal’s probability distribution obeys the exponential distribution, and mostly are small signals. To increase the quantization SNR (signal-to-noise ratio) and reduce the quantization error, it is necessary to increase Quantization regions, which leads to increase in coding complexity.

2)  Given a set of representation points {aj }, how should the intervals {Rj } be chosen?

The answer is simple: we choose bj to be the midpoint between aj and aj+1, obviously, when u>bj, u is closer to aj+1 than aj.

3)  Given a set of intervals {Rj }, how should the representation points {aj } be chosen?

Obviously: each aj must be the mean of an rv Uj with pdf fj (u). In other words, aj must be the conditional mean of U conditional on U ∈Rj.

4.   The Lloyd-Max algorithm

Combine the two questions in the previous part of non-uniform quantization:

综合非均匀划分的两个问题：