平衡树模板【splay的实现】

【平衡树splay实现】

无注释代码

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int INF=1e9+,MAXN=1e5+;
 int N;
 int key[MAXN],cnt[MAXN],ch[MAXN][],siz[MAXN],f[MAXN];
 int root,sz;
 inline void clear(int x){
     key[x]=cnt[x]=ch[x][]=ch[x][]=siz[x]=f[x]=;
 }
 inline int get(int x){
     return x==ch[f[x]][];
 }
 inline void upd(int x){
     if(x){
         siz[x]=cnt[x];
         if(ch[x][]){
             siz[x]+=siz[ch[x][]];
         }
         if(ch[x][]){
             siz[x]+=siz[ch[x][]];
         }
     }
 }
 inline void rotate(int x){
     int fa=f[x],gf=f[fa],which=get(x);
     ch[fa][which]=ch[x][which^];
     f[ch[fa][which]]=fa;
     ch[x][which^]=fa;
     f[fa]=x;
     f[x]=gf;
     if(gf){
         ch[gf][ch[gf][]==fa]=x;
     }
     upd(fa);
     upd(x);
 }
 inline void splay(int x){
     for(int fa;(fa=f[x]);rotate(x)){
         if(f[fa]){
             rotate(get(x)==get(fa)?fa:x);
         }
     }
     root=x;
 }
 inline void ins(int x){
     if(!root){
         sz++;
         clear(sz);
         root=sz;
         cnt[sz]=siz[sz]=;
         key[sz]=x;
         return;
     }
     int cur=root,fa=;
     while(){
         if(x==key[cur]){
             cnt[cur]++;
             upd(cur);
             upd(fa);
             splay(cur);
             return;
         }
         fa=cur;
         cur=ch[fa][key[fa]<x];
         if(!cur){
             clear(++sz);
             f[sz]=fa;
             cnt[sz]=siz[sz]=;
             ch[fa][key[fa]<x]=sz;
             key[sz]=x;
             upd(fa);
             splay(sz);
             return;
         }
     }
 }
 inline int find(int x){
     int cur=root,ret=;
     while(){
         if(x<key[cur]){
             cur=ch[cur][];
         }else{
             ret+=(ch[cur][]?siz[ch[cur][]]:);
             if(key[cur]==x){
                 splay(cur);
                 return ret+;
             }
             ret+=cnt[cur];
             cur=ch[cur][];
         }
     }
 }
 inline int findx(int x){
     int cur=root;
     while(){
         if(ch[cur][]&&x<=siz[ch[cur][]]){
             cur=ch[cur][];
         }else{
             int tmp=(ch[cur][]?siz[ch[cur][]]:)+cnt[cur];
             if(x<=tmp){
                 return key[cur];
             }
             x-=tmp;
             cur=ch[cur][];
         }
     }
 }
 inline int pre(){
     int cur=ch[root][];
     while(ch[cur][]){
         cur=ch[cur][];
     }
     return cur;
 }
 inline int nxt(){
     int cur=ch[root][];
     while(ch[cur][]){
         cur=ch[cur][];
     }
     return cur;
 }
 inline void del(int x){
     find(x);
     if(cnt[root]>){
         cnt[root]--;
         upd(root);
         return;
     }
     if(!ch[root][]&&!ch[root][]){
         clear(root);
         root=;
         return;
     }
     if(!ch[root][]){
         int old=root;
         root=ch[root][];
         f[root]=;
         clear(old);
         return;
     }
     if(!ch[root][]){
         int old=root;
         root=ch[root][];
         f[root]=;
         clear(old);
         return;
     }
     int old=root,p=pre();
     splay(p);
     ch[root][]=ch[old][];
     f[ch[old][]]=root;
     clear(old);
     upd(root);
 }
 int main(){
     scanf("%d",&N);
     for(int i=;i<=N;i++){
         int ii,jj;
         scanf("%d%d",&ii,&jj);
         switch(ii){
             case :{
                 ins(jj);
                 break;
             }
             case :{
                 del(jj);
                 break;
             }
             case :{
                 printf("%d\n",find(jj));
                 break;
             }
             case :{
                 printf("%d\n",findx(jj));
                 break;
             }
             case :{
                 ins(jj);
                 printf("%d\n",key[pre()]);
                 del(jj);
                 break;
             }
             case :{
                 ins(jj);
                 printf("%d\n",key[nxt()]);
                 del(jj);
                 break;
             }
         }
     }
     return ;
 }

变量声明：f[i]表示i的父结点，ch[i][0]表示i的左儿子，ch[i][1]表示i的右儿子，key[i]表示i的关键字（即结点i代表的那个数字），cnt[i]表示i结点的关键字出现的次数（相当于权值），size[i]表示包括i的这个子树的大小；sz为整棵树的大小，root为整棵树的根。

再介绍几个基本操作：

【clear操作】：将当前点的各项值都清0（用于删除之后）

inline void clear(int x){/*清空节点中的数据*/
    key[x]=cnt[x]=ch[x][]=ch[x][]=siz[x]=f[x]=;
}

【get操作】：判断当前点是它父结点的左儿子还是右儿子

inline int get(int x){/*查询当前点是否为右孩子*/
    return x==ch[f[x]][];
}

【update操作】：更新当前点的size值（用于发生修改之后）

inline void upd(int x){/*更新cnt和siz数组*/
    if(x){
        siz[x]=cnt[x];
        if(ch[x][]){
            siz[x]+=siz[ch[x][]];
        }
        if(ch[x][]){
            siz[x]+=siz[ch[x][]];
        }
    }
}

【rotate操作】

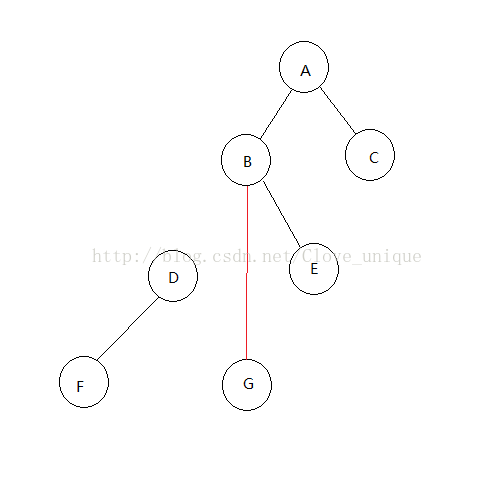
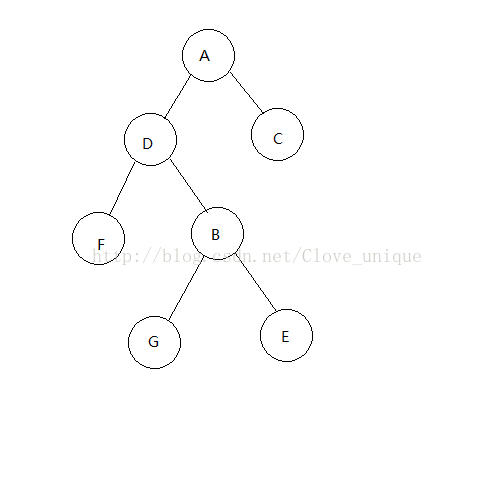
这是原来的树，假设我们现在要将D结点rotate到它的父亲的位置。

step 1：

找出D的父亲结点（B）以及父亲的父亲（A）并记录。判断D是B的左结点还是右结点。

step 2：

我们知道要将Drotate到B的位置，二叉树的大小关系不变的话，B就要成为D的右结点了没错吧？

咦？可是D已经有右结点了，这样不就冲突了吗？怎么解决这个冲突呢？

我们知道，D原来是B的左结点，那么rotate过后B就一定没有左结点了对吧，那么正好，我们把G接到B的左结点去，并且这样大小关系依然是不变的，就完美的解决了这个冲突。

这样我们就完成了一次rotate，如果是右儿子的话同理。step 2的具体操作：

我们已经判断了D是B的左儿子还是右儿子，设这个关系为K；将D与K关系相反的儿子的父亲记为B与K关系相同的儿子（这里即为D的右儿子的父亲记为B的左儿子）；将D与K关系相反的儿子的父亲即为B（这里即为把G的父亲记为B）；将B的父亲即为D；将D与K关系相反的儿子记为B（这里即为把D的右儿子记为B）；将D的父亲记为A。

最后要判断，如果A存在（即rotate到的位置不是根的话），要把A的儿子即为D。

显而易见，rotate之后所有牵涉到变化的父子关系都要改变。以上的树需要改变四对父子关系，BG DG BD AB，需要三个操作（BG BD AB）。

step 3：update一下当前点和各个父结点的各个值

inline void rotate(int x){
    int fa=f[x]/*父亲*/,gf=f[fa]/*祖父*/,which=get(x);
    ch[fa][which]=ch[x][which^];
    f[ch[fa][which]]=fa;
    ch[x][which^]=fa;
    f[fa]=x;
    f[x]=gf;
    if(gf){
        ch[gf][ch[gf][]==fa]=x;
    }
    upd(fa);/*先更新在下面的节点*/
    upd(x);
}

【splay操作】

其实splay只是rotate的发展。伸展操作只是在不停的rotate，一直到达到目标状态。如果有一个确定的目标状态，也可以传两个参。此代码直接splay到根。

splay的过程中需要分类讨论，如果是三点一线的话（x，x的父亲，x的祖父）需要先rotate x的父亲，否则需要先rotate x本身（否则会形成单旋使平衡树失衡）

inline void splay(int x){
    for(int fa;(fa=f[x]);rotate(x)){
//        printf("fa[%d]=%d\n",fa,f[fa]);
        if(f[fa]){
            rotate(get(x)==get(fa)?fa:x);/*三点一线先rotate父亲*/
        }
    }
    root=x;
}

【insert操作】

其实插入操作是比较简单的，和普通的二叉查找树基本一样。

step 1：如果root=0，即树为空的话，做一些特殊的处理，直接返回即可。

step 2：按照二叉查找树的方法一直向下找，其中：

如果遇到一个结点的关键字等于当前要插入的点的话，我们就等于把这个结点加了一个权值。因为在二叉搜索树中是不可能出现两个相同的点的。并且要将当前点和它父亲结点的各项值更新一下。做一下splay。

如果已经到了最底下了，那么就可以直接插入。整个树的大小要+1，新结点的左儿子右儿子（虽然是空）父亲还有各项值要一一对应。并且最后要做一下他父亲的update（做他自己的没有必要）。做一下splay。

inline void ins(int x){
    if(!root){
        sz++;
        clear(sz);
        root=sz;
        cnt[sz]=siz[sz]=;
        key[sz]=x;
        return;
    }
    int cur=root,fa=;
    while(){
        if(x==key[cur]){
            cnt[cur]++;
            upd(cur);
            upd(fa);
            splay(cur);
            return;
        }
        fa=cur;
        cur=ch[fa][key[fa]<x];
        if(!cur){
            clear(++sz);
            f[sz]=fa;
            cnt[sz]=siz[sz]=;
            ch[fa][key[fa]<x]=sz;
            key[sz]=x;
            upd(fa);
            splay(sz);
            return;
        }
    }
}

【find操作】查询x的排名

初始化：ans=0，当前点=root

和其它二叉搜索树的操作基本一样。但是区别是：

如果x比当前结点小，即应该向左子树寻找，ans不用改变（设想一下，走到整棵树的最左端最底端排名不就是1吗）。

如果x比当前结点大，即应该向右子树寻找，ans需要加上左子树的大小以及根的大小（这里的大小指的是权值）。

不要忘记了再splay一下

inline int find(int x){
    int cur=root,ret=;
    while(){
        if(x<key[cur]){
            cur=ch[cur][];
        }else{
            ret+=(ch[cur][]?siz[ch[cur][]]:);
            if(key[cur]==x){
                splay(cur);
                return ret+;
            }
            ret+=cnt[cur];
            cur=ch[cur][];
        }
    }
}

【findx操作】找到排名为x的点

初始化：当前点=root

和上面的思路基本相同：

如果当前点有左子树，并且x比左子树的大小小的话，即向左子树寻找；

否则，向右子树寻找：先判断是否有右子树，然后记录右子树的大小以及当前点的大小（都为权值），用于判断是否需要继续向右子树寻找。

inline int findx(int x){
    int cur=root;
    while(){
        if(ch[cur][]&&x<=siz[ch[cur][]]){
            cur=ch[cur][];
        }else{
            int tmp=(ch[cur][]?siz[ch[cur][]]:)+cnt[cur];
            if(x<=tmp){
                return key[cur];
            }
            x-=tmp;
            cur=ch[cur][];
        }
    }
}

【求x的前驱（后继），前驱（后继）定义为小于（大于）x，且最大（最小）的数】

这类问题可以转化为将x插入，求出树上的前驱（后继），再将x删除的问题。

其中insert操作上文已经提到。

【pre/next操作】

这个操作十分的简单，只需要理解一点：在我们做insert操作之后做了一遍splay。这就意味着我们把x已经splay到根了。求x的前驱其实就是求x的左子树的最右边的一个结点，后继是求x的右子树的左边一个结点（想一想为什么？）

inline int pre(){
    int cur=ch[root][];
    while(ch[cur][]){
        cur=ch[cur][];
    }
    return cur;
}

inline int nxt(){
    int cur=ch[root][];
    while(ch[cur][]){
        cur=ch[cur][];
    }
    return cur;
}

【del操作】

删除操作是最后一个稍微有点麻烦的操作。

step 1：随便find一下x。目的是：将x旋转到根。

step 2：那么现在x就是根了。如果cnt[root]>1，即不只有一个x的话，直接-1返回。

step 3：如果root并没有孩子，就说名树上只有一个x而已，直接clear返回。

step 4：如果root只有左儿子或者右儿子，那么直接clear root，然后把唯一的儿子当作根就可以了（f赋0，root赋为唯一的儿子）

剩下的就是它有两个儿子的情况。

step 5：我们找到新根，也就是x的前驱（x左子树最大的一个点），将它旋转到根。然后将原来x的右子树接到新根的右子树上（注意这个操作需要改变父子关系）。这实际上就把x删除了。不要忘了update新根。

inline void del(int x){
    find(x);
    if(cnt[root]>){
        cnt[root]--;
        upd(root);
        return;
    }
    if(!ch[root][]&&!ch[root][]){
        clear(root);
        root=;
        return;
    }
    if(!ch[root][]){
        int old=root;
        root=ch[root][];
        f[root]=;
        clear(old);
        return;
    }
    if(!ch[root][]){
        int old=root;
        root=ch[root][];
        f[root]=;
        clear(old);
        return;
    }
    int old=root,p=pre();
    splay(p);
    ch[root][]=ch[old][];
    f[ch[old][]]=root;
    clear(old);
    upd(root);
}

【总结】

平衡树的本质其实是二叉搜索树，所以很多操作是基于二叉搜索树的操作。

splay的本质是rotate，旋转其实只是为了保证二叉搜索树的平衡性。

所有的操作一定都满足二叉搜索树的性质，所有改变父子关系的操作一定要update。

关键是理解rotate，splay的原理以及每一个操作的原理。

转载自原文

【完整代码】

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int INF=1e9+,MAXN=1e5+;
 int N;
 int key[MAXN]/*关键字|值*/,cnt[MAXN]/*关键字数量*/,ch[MAXN][]/*儿子的下标*/,siz[MAXN],f[MAXN];
 int root/*根*/,sz/*节点栈顶*/;/*splay的数组空间不能重复利用*/
 inline void DEBUG(){
     printf("root=%d siz=%d\n",root,sz);
     for(int i=;i<=sz;i++){
         printf("(idx=%d,cnt=%d,siz=%d,key=%d,f=%d,lc=%d,rc=%d)\n",i,cnt[i],siz[i],key[i],f[i],ch[i][],ch[i][]);
     }
     puts("-------------------------------------------------------");
 }
 inline void clear(int x){/*清除节点中的数据*/
     key[x]=cnt[x]=ch[x][]=ch[x][]=siz[x]=f[x]=;
 }
 inline int get(int x){/*查询当前节点是否为右孩子*/
     return x==ch[f[x]][];
 }
 inline void upd(int x){
     if(x){
         siz[x]=cnt[x];
         if(ch[x][]){
             siz[x]+=siz[ch[x][]];
         }
         if(ch[x][]){
             siz[x]+=siz[ch[x][]];
         }
     }
 }
 inline void rotate(int x){
     int fa=f[x]/*父亲下标*/,gf=f[fa]/*祖父*/,which=get(x);
     ch[fa][which]=ch[x][which^];
     f[ch[fa][which]]=fa;
     ch[x][which^]=fa;
     f[fa]=x;
     f[x]=gf;
     if(gf){
         ch[gf][ch[gf][]==fa]=x;
     }
     upd(fa);/*先更新下方节点*/
     upd(x);
 }
 inline void splay(int x){
     for(int fa;(fa=f[x]);rotate(x)){
         if(f[fa]){
             rotate(get(x)==get(fa)?fa:x);/*三点一线先rotate父亲*/
         }
     }
     root=x;
 }
 inline void ins(int x){
     if(!root){
         sz++;
         clear(sz);
         root=sz;
         cnt[sz]=siz[sz]=;
         key[sz]=x;
         return;
     }
     int cur=root,fa=;
     while(){
         if(x==key[cur]){
             cnt[cur]++;
             upd(cur);
             upd(fa);
             splay(cur);
             return;
         }
         fa=cur;
         cur=ch[fa][key[fa]<x];
         if(!cur){
             clear(++sz);
             f[sz]=fa;
             cnt[sz]=siz[sz]=;
             ch[fa][key[fa]<x]=sz;
             key[sz]=x;
             upd(fa);
             splay(sz);
             return;
         }
     }
 }
 inline int find(int x){
     int cur=root,ret=;
     while(){
         if(x<key[cur]){
             cur=ch[cur][];
         }else{
             ret+=(ch[cur][]?siz[ch[cur][]]:);
             if(key[cur]==x){
                 splay(cur);
                 return ret+;
             }
             ret+=cnt[cur];
             cur=ch[cur][];
         }
     }
 }
 inline int findx(int x){
     int cur=root;
     while(){
         if(ch[cur][]&&x<=siz[ch[cur][]]){
             cur=ch[cur][];
         }else{
             int tmp=(ch[cur][]?siz[ch[cur][]]:)+cnt[cur];
             if(x<=tmp){
                 return key[cur];
             }
             x-=tmp;
             cur=ch[cur][];
         }
     }
 }
 inline int pre(){
     int cur=ch[root][];
     while(ch[cur][]){
         cur=ch[cur][];
     }
     return cur;
 }
 inline int nxt(){
     int cur=ch[root][];
     while(ch[cur][]){
         cur=ch[cur][];
     }
     return cur;
 }
 inline void del(int x){
     find(x);
     if(cnt[root]>){
         cnt[root]--;
         upd(root);
         return;
     }
     if(!ch[root][]&&!ch[root][]){
         clear(root);
         root=;
         return;
     }
     if(!ch[root][]){
         int old=root;
         root=ch[root][];
         f[root]=;
         clear(old);
         return;
     }
     if(!ch[root][]){
         int old=root;
         root=ch[root][];
         f[root]=;
         clear(old);
         return;
     }
     int old=root,p=pre();
     splay(p);
     ch[root][]=ch[old][];
     f[ch[old][]]=root;
     clear(old);
     upd(root);
 }
 int main(){
     scanf("%d",&N);
     for(int i=;i<=N;i++){
         int ii,jj;
         scanf("%d%d",&ii,&jj);
         switch(ii){
             case :{/*插入x数*/
                 ins(jj);
                 break;
             }
             case :{/*删除x数*/
                 del(jj);
                 break;
             }
             case :{/*查询x数的排名*/
                 printf("%d\n",find(jj));
                 break;
             }
             case :{/*查询排名为x的数*/
                 printf("%d\n",findx(jj));
                 break;
             }
             case :{/*求x的前驱*/
                 ins(jj);
                 printf("%d\n",key[pre()]);
                 del(jj);
                 break;
             }
             case :{/*求x的后继*/
                 ins(jj);
                 printf("%d\n",key[nxt()]);
                 del(jj);
                 break;
             }
         }
     }
     return ;
 }

无注释代码