Codeforces Round #606 (Div. 2) - E. Two Fairs(割点+dfs)

题意：给你一张无向连通图，对于求有多少对$(x,y)$满足互相到达必须经过$(a,b)$，其中$x\neq a,x\neq b,y\neq a,y\neq b$

思路：显然$a,b$都必须为割点，所以先用$tarjan$判断$a,b$是否都为割点，如果$a$或$b$有一个不为割点，那么答案就是$0$

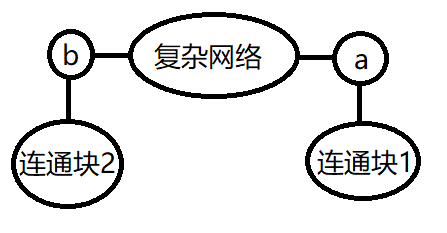
当$a,b$都为割点时，答案为连通块$1$内点的个数$*$连通块$2$内点的个数，以求连通块$1$内点的个数为例，从$b$点开始$dfs$，当遇到$a$点时停止，统计出$($连通块$2+$复杂网络$+b+a)$这些点的个数，连通块$1$内点的个数就是用$n$减去$dfs$求出的点的个数，求连通块$2$内点的个数从$a$点开始$dfs$即可。

#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = ;

typedef long long ll;

struct node {
    int to, nex;
};

node edge[ * N];
int t, n, m, a, b, cnt, head[N];
int dfn[N], timing, pcut[N];
int cnta, cntb, vis[N];

void dfs(int u, int mk, int a, int b)
{
    vis[u] = ;
    if ( == mk) cnta++;
    if ( == mk) cntb++;
    if ( == mk && u == b) return;
    if ( == mk && u == a) return;
    for (int i = head[u];  != i; i = edge[i].nex) {
        int v = edge[i].to;
        if (!vis[v]) dfs(v, mk, a, b);
    }
    return;
}

void add_edge(int u, int v)
{
    edge[++cnt].to = v;
    edge[cnt].nex = head[u];
    head[u] = cnt;
}

int tarjan(int u, int fa)
{
    int child = , lowu;
    lowu = dfn[u] = ++timing;
    for (int i = head[u];  != i; i = edge[i].nex) {
        int v = edge[i].to;
        if (!dfn[v]) {
            child++;
            int lowv = tarjan(v, u);
            if (lowv >= dfn[u] && u != fa) pcut[u] = ;
            lowu = min(lowu, lowv);
        }
        else if (v != fa) {
            lowu = min(lowu, dfn[v]);
        }
    }
    if (u == fa && child > ) pcut[u] = ;
    return lowu;
}

void init()
{
    cnt = timing = cnta = cntb = ;
    for (int i = ; i <= n; i++)
        pcut[i] = dfn[i] = head[i] = ;
}

int main()
{
    scanf("%d", &t);
    while (t--) {
        scanf("%d%d%d%d", &n, &m, &a, &b);
        init();
        for (int i = ; i <= m; i++) {
            int u, v;
            scanf("%d%d", &u, &v);
            add_edge(u, v), add_edge(v, u);
        }
        for (int i = ; i <= n; i++) {
            if ( == dfn[i]) tarjan(i, i);
        }
        if ( == pcut[a] ||  == pcut[b]) {
            printf("0\n");
            continue;
        }
        for (int i = ; i <= n; i++) vis[i] = ;
        dfs(a, , a, b);
        for (int i = ; i <= n; i++) vis[i] = ;
        dfs(b, , a, b);
        ll x = ll(n - cnta), y = ll(n - cntb);
        printf("%lld\n", x * y);
    }
    return ;
}