浅谈DFS,BFS,IDFS,A*等算法

搜索是编程的基础，是必须掌握的技能。——王主任

搜索分为盲目搜索和启发搜索

下面列举OI常用的盲目搜索：

1. dijkstra
2. SPFA
3. bfs
4. dfs
5. 双向bfs
6. 迭代加深搜索(IDFS)

下面列举OI常用的启发搜索：

1. 最佳优先搜索(A)
2. A*
3. IDA*

那么什么是盲目，什么是启发？

举个例子，假如你在学校操场，老师叫你去国旗那集合，你会怎么走？
假设你是瞎子，你看不到周围，那如果你运气差，那你可能需要把整个操场走完才能找到国旗。这便是盲目式搜索，即使知道目标地点，你可能也要走完整个地图。
假设你眼睛没问题，你看得到国旗，那我们只需要向着国旗的方向走就行了，我们不会傻到往国旗相反反向走，那没有意义。
这种有目的的走法，便被称为启发式的。

左图为bfs，右图为A

提供一个搜索可视化的链接https://qiao.github.io/PathFinding.js/visual/

搜索算法浅谈

DFS

    基础中的基础，几乎所有题都可以出一档指数级复杂度暴力分给DFS，同时他的实现也是目录中提到的所有搜索算法中最简单的

dfs的核心思想是：不撞南墙不回头    孙学凤:物理人不撞南墙

举个例子：



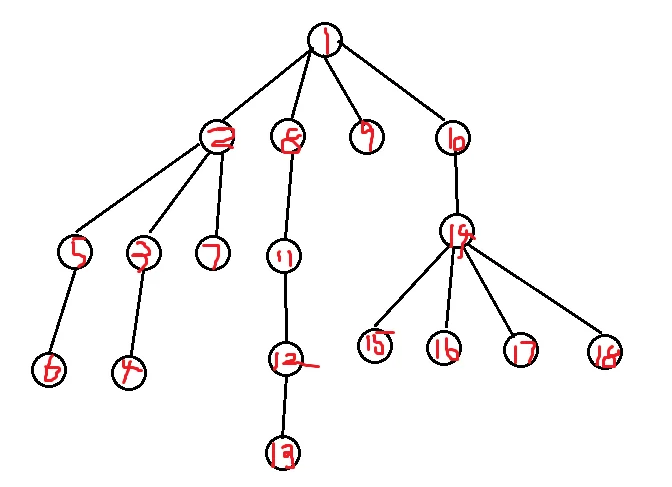
你现在在一号点，你想找到树中与一号点连通的每一个点

那么我们考虑按照深度优先的顺序去遍历这棵树，即，假设你当前在点x，如果和x连边的点中有一个点y，满足y比x深，即y是x的儿子，并且y还没有被访问过，那么我们就走到y，如果有多个y满足条件，我们走到其中任意一个

如果没有y满足条件，我们返回x的父亲

按照这个顺序，我们就可以访问到每个节点，并且每条边会恰好被走两次（从父亲到儿子一次，从儿子到父亲一次）

由于dfs的特性，它有时候会非常的浪费时间，为什么呢？

还是刚才这张图：



如果我们把终点设在10号点，在dfs的过程中要先搜完一号点及其三个子树才能到达终点

代码大体框架：

void dfs(int k){
    if(到达目的地或满足条件)输出解
    for(int i=1;i<=算符种数;++i){
        保存结果//有时候不需要
        dfs(k+1);
        回溯结果//有时候不需要
    }
}

那么什么时候需要回溯呢？

我们先要了解回溯的目的：

  我们在搜索的过程中，先选择一种可能的情况向前搜索，一旦发现选择的结果是错误的，就退一步重新选择，这就需要回溯，向前搜索一步之后将状态恢复成之前的样子

所以在解题的过程中要判断好是否需要回溯

bfs

bfs利用了一种线性数据结构，队列

bfs的核心思想是:从厨师节点开始，生成第一层节点，检查目标节点是否在目标节点中，若没有再将第一层所有的节点逐一扩展，如此往复知道发现目标节点为止

我们再拿出徐瑞帆dalao的图：



你现在还是在一号点，你还是想找到树中与一号点连通的每一个点

我们初始的时候把一号点推入队取出队尾，然后只要当前队列非空，我们就取出队头元素x，并将队头弹出

然后我们将x的所有儿子推入队列

对于图上的情况，我们将所有与x相连，并且还没入过队的点推入队列

这样我们就能够访问所有点

代码大致框架:

void bfs(){
    q.push(head);
    while(!q.empty()){
        temp=q.front;
        q.pop();
        if(temp为目标状态)输出解
        if(temp不合法)continue;
        if(temp合法)q.push(temp+Δ);
    }
}

IDFS

我们已经学会了dfs和bfs

然而有的问题还是使我们无法进行搜索，因为你要进行搜索的图可能是无限大的，每个点所连的边也可能是无限多的，这就使得dfs和bfs都失效了，这时候我们就需要用到idfs

我们枚举深搜的时候深度的上限，因为深度上限的限制，图中的一些边会被删掉，而图就变成了一个有限的图，我们就可以进行dfs了

举个栗子:



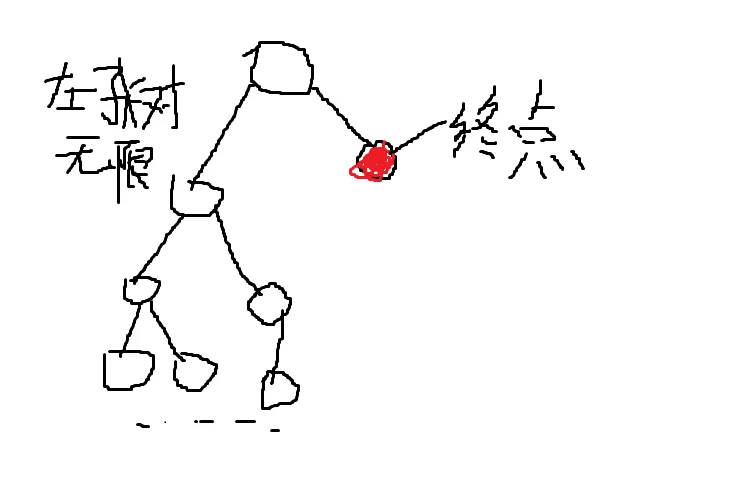
如果用普通的dfs，这显然是一个无解的情况，你将会陷入无限的左子树中

这时，我们设一个深度d，每次搜到第d层就返回搜其他的分支。如果在d层没搜到答案则d++，从头再搜

然而这个算法有一个很明显的缺陷，有一些非答案点要重复搜好几遍，这造成了极大的浪费

于是我们有了IDA*

A*

在看IDA* 之前，我们先了解A*

搜索算法经常运行效率很低，为了提高效率，我们可以使用A*算法

我们对每个点定义一个估价函数f(x)=g(x)+h(x)

g(x)表示从起始点到x的实际代价

h(x)表示估计的从x到结束点的代价，并要求h(x)小于等于从x到结束点的实际代价

那么每次我们从可行点集合中找到f(x)最小的x，然后搜索他

这个过程可以用优先队列（即堆）实现

这样的话可以更快地到达结束点，并保证到达结束点时走的是最优路径

为什么要求h(x)小于等于实际代价呢？

因为如果h(x)大于实际代价的话，可能以一条非最优的路径走到结束点，导致答案变大

举个栗子:用A*做的八数码难题

#include<map>
#include<queue>
#include<iostream>
#include<algorithm>
using namespace std;
int dx[]={-1,0,0,1},dy[]={0,-1,1,0};
int final[]={-1,0,1,2,5,8,7,6,3};
struct node
{
	int state,g,h;
	node(int _state,int _g)
	{
		state=_state;
		g=_g;
		h=0;
		int tmp=state;
		for(int i=8;i>=0;i--)
		{
			int a=tmp%10;tmp/=10;
			if(a!=0)h+=abs((i/3)-(final[a]/3))+abs((i%3)-(final[a]%3));
		}
	}
};
bool operator<(node x,node y)
{
	return x.g+x.h>y.g+y.h;
}
priority_queue<node>q;
map<int,bool>vis;
int main()
{
	int n;
	cin>>n;
	q.push(node(n,0));
	vis[n]=1;
	while(!q.empty())
	{
		node u=q.top();
		int c[3][3],f=0,g=0,n=u.state;q.pop();
		if(u.state==123804765)
		{
			cout<<u.g<<endl;
			return 0;
		}
		for(int i=2;i>=0;i--)
		for(int j=2;j>=0;j--)
		{
			c[i][j]=n%10,n/=10;
			if(!c[i][j])f=i,g=j;
		}
		for(int i=0;i<4;i++)
		{
			int nx=f+dx[i],ny=g+dy[i],ns=0;
			if(nx<0||ny<0||nx>2||ny>2)continue;
			swap(c[nx][ny],c[f][g]);
			for(int i=0;i<3;i++)
			for(int j=0;j<3;j++)
			ns=ns*10+c[i][j];
			if(!vis.count(ns))
			{
				vis[ns]=1;
				q.push(node(ns,u.g+1));
			}
			swap(c[nx][ny],c[f][g]);
		}
	}
}

这是bfs做法



这是A*做法

很明显，A*比bfs快多了

值得注意的是，A*只能在有解的情况下使用

IDA*

在进行IDFS的时候，我们也可以用A*进行搜索

如果在当前深度限制下搜到了结束状态，我们就可以直接输出答案

代码大体框架:

//1代表墙，0代表空地，2代表终点
int G[maxn][maxn];
int n, m;
int endx, endy;
int maxd;
const int dx[4] = { -1, 1, 0, 0 };
const int dy[4] = { 0, 0, -1, 1 };
namespace ida
{
    bool dfs(int x, int y, int d);
    inline int h(int x, int y);
    bool ida_star(int x, int y, int d)
    {
        if (d == maxd)                   //是否搜到答案
        {
            if (G[x][y] == 2)
                return true;
            return false;
        }
        int f = h(x, y) + d;          //评估函数
        if (f > maxd)                //maxd为最大深度
            return false;
    //尝试向左，向右,向上，向下走
        for (int i = 0; i < 4; i++)
        {
            int next_x = x + dx[i];
            int next_y = y + dy[i];
            if (next_x > n || next_x < 1 || next_y > m || next_y < 1 || G[next_x][next_y] == 1)
                continue;
            if (ida_star(next_x, next_y, d + 1))
                return true;
        }
        return false;
    }
    inline int h(int x, int y)
    {
        return abs(x - endx) + abs(y - endy);
    }
}