Lining Up

AtCoder - 2271-Lining Up
           
           
               
                   
                    原创                                                                                                                                            fadedsun
                    最后发布于2017-08-07 10:10:15                   
                    阅读数 656
                   
                       
                        收藏
                   
               
                               
               
               
                                                                展开
                                   
           
       
   
   
       
               
               
                                   
        
           
                                       
                   
                   
                                            Problem Statement
There are N people, conveniently numbered 1 through N. They were standing in a row yesterday, but now they are unsure of the order in which they were standing. However, each person remembered the following fact: the absolute difference of the number of the people who were standing to the left of that person, and the number of the people who were standing to the right of that person. According to their reports, the difference above for person i is Ai.

Based on these reports, find the number of the possible orders in which they were standing. Since it can be extremely large, print the answer modulo 109+7. Note that the reports may be incorrect and thus there may be no consistent order. In such a case, print 0.

Constraints
1≦N≦105
0≦Ai≦N−1
Input
The input is given from Standard Input in the following format:

N
A1 A2 … AN
Output
Print the number of the possible orders in which they were standing, modulo 109+7.

Sample Input 1
5
2 4 4 0 2
Sample Output 1
4
There are four possible orders, as follows:

2,1,4,5,3
2,5,4,1,3
3,1,4,5,2
3,5,4,1,2
Sample Input 2
7
6 4 0 2 4 0 2
Sample Output 2
0
Any order would be inconsistent with the reports, thus the answer is 0.

Sample Input 3
8
7 5 1 1 7 3 5 3
Sample Output 3
16

 

题意：

有n个人，他们只记得昨天站在他们右边的人和站在左边的人的人数差值。根据差值，问有多少种可能的站法。

 

解题思路：

首先分奇数和偶数讨论。

1.奇数：站在中间的人，左右相差的人数肯定一样多，所以为0.且0只会有一个。
       从中间往俩边延伸，可以知道每移动一位，那么差的人数增加2；
       那么奇数情况下，只会有0，2，4，6，8.且0只有一个。其它2个。

2.偶数情况，可以知道没有为0的人。从1开始。1，3，5，7，。个数都为2.

因为0，肯定站中间，不用管，其他的左右对称，出现次数肯定为2.
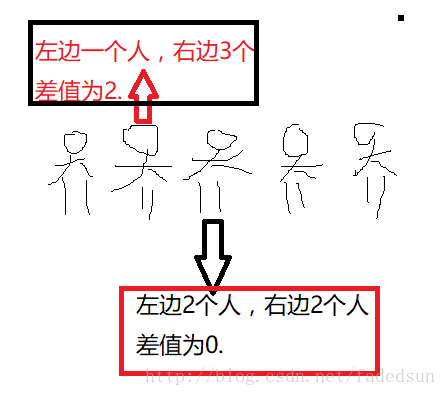
如果可以，因为，位置有俩个，一个站的位置确定，另一个人就确定了，
那么根据组合排列中的乘法原理，就可得知。

 

 

注意点：

记得取模
判断出现次数是否符合规则
小心数据太大溢出
取模要根据乘法取模规则

# include <cstdio>
# include <map>
# include <cmath>

using namespace std;

const int mod = 1e9+;

int main()
{
    int n;
    int  a[];
    map<int,int> m;
    scanf("%d",&n);

    for(int i = ;i < n;i++)
    {
        scanf("%d",&a[i]);
        m[a[i]]++;
    }

    int flag = ;
    if(n%) //奇数
    {
        if(m[] != )
        {
            flag = ;
        }
        for(int i = ;i < n;i+=)
        {
            if(m[i] != )
            {
                flag = ;
            }
        }
    }else{
        for(int i = ;i < n;i+=)
        {
            if(m[i] != )
            {
                flag = ;
            }
        }
    }
    long long sum = ;

    for(int i =;i < floor(n/);i++)
    {
        sum = ((sum % mod) * )% mod;
    }

    if(n%)
    {
        if(flag)
        printf("0\n");
        else
        printf("%lld\n",sum);
    }
    else
    {
        if(flag)
        printf("0\n");
        else
        printf("%lld\n",sum);
    }

    return ;
 }