hdu4352-XHXJ's LIS状压DP+数位DP
(有任何问题欢迎留言或私聊 && 欢迎交流讨论哦
题意:传送门
原题目描述在最下面。
在区间内把整数看成一个阿拉伯数字的集合,此集合中最长严格上升子序列的长度为k的个数。
思路:
看了大神的博客感觉这东西是真难想到。状压dp预处理状态,数位dp计算答案。
nex[i][j]表示在状态i(状态i的二进制中为1表示这个数存在LIS中,反之不存在),选取加入第j的数字之后的状态。
然后这题k最大也只有10,因为只有10个数字。所以状态只有1024种。这题还要处理一下前导0。
AC代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<bitset>
#define lowbit(x) x&(-x)
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int mod = 1e9;
const int N = (int)1e2+7;
LL n, m, k;
int one[1<<10], ar[30], nex[1<<10][10];
LL dp[30][1<<10][11];
int get(int x, int y){
for(int i = y; i < 10; ++i){
if(x&(1<<i)) return (x^(1<<i))|(1<<y);
}
return x|(1<<y);
}
void init(){
for(int i = 0; i < (1<<10); ++i){
for(int j = 0; j < 10; ++j){
if(i&(1<<j))one[i]++;
nex[i][j] = get(i, j);
}
}
memset(dp,-1,sizeof(dp));
}
LL dfs(int pos, int sta, bool lead, bool limit){
if(pos == -1)return one[sta] == k;
if(!limit&&!lead&&dp[pos][sta][k] != -1) return dp[pos][sta][k];
int up = limit? ar[pos]: 9;
LL sum = 0;
for(int i = 0; i <= up; ++i){
sum +=dfs(pos-1,(lead&&i==0)?0:nex[sta][i],lead&i==0,limit&&i==ar[pos]);
}
if(!limit&&!lead)dp[pos][sta][k] = sum;
return sum;
}
LL solve(LL x){
int pos = 0;
while(x){ar[pos++]=x%10;x/=10;}
return dfs(pos-1,0,1,1);
}
int main(){
init();
int tim,tca=0;
scanf("%d", &tim);
while(tim--){
scanf("%lld%lld%lld", &n, &m, &k);
printf("Case #%d: %lld\n", ++tca, solve(m)-solve(n-1));
}
return 0;
}
####原题目描述:
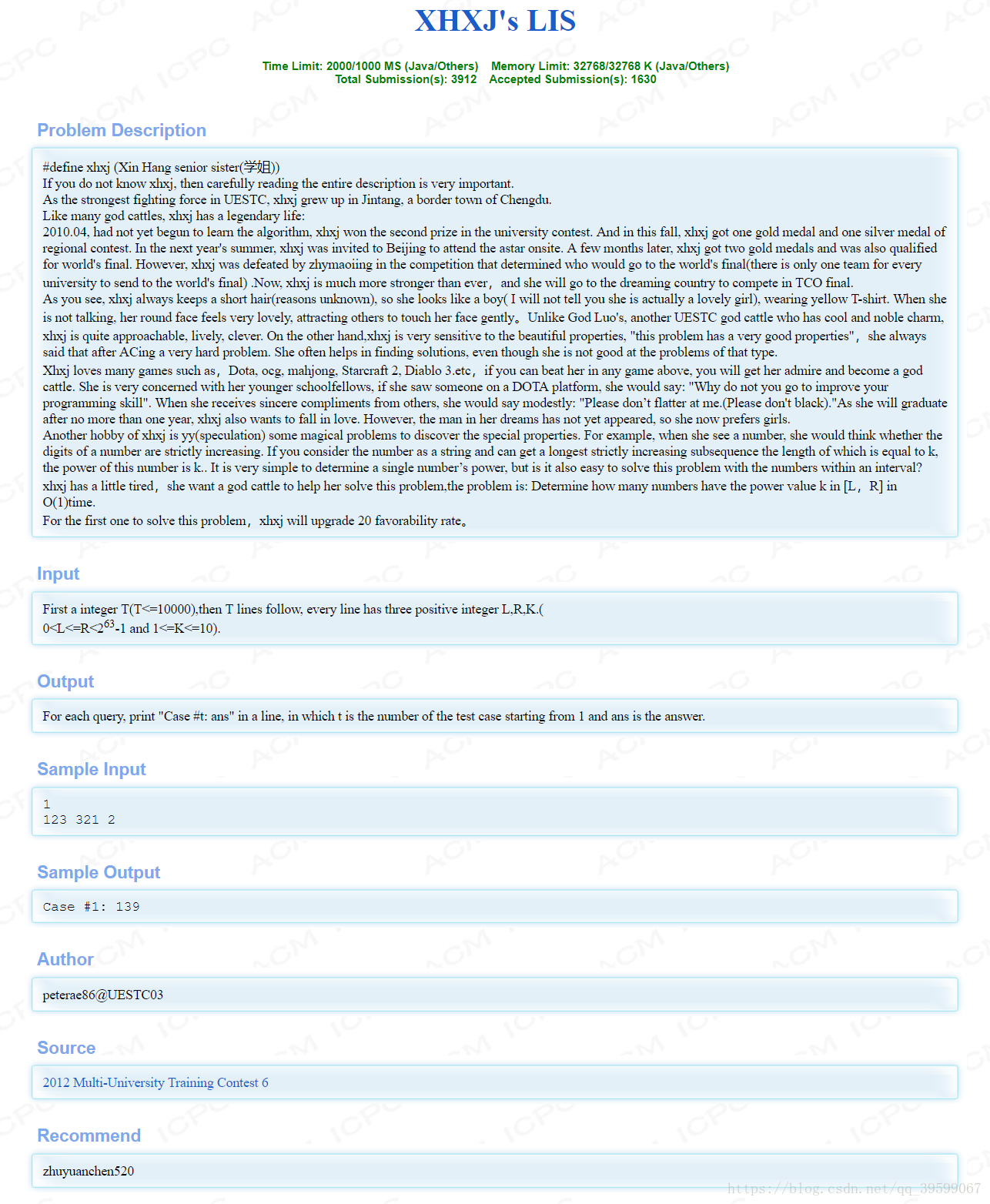
hdu4352-XHXJ's LIS状压DP+数位DP的更多相关文章
- HDU 4352 XHXJ's LIS - 状压dp + LIS
传送门 题目大意: 求[l, r]中数位的最长上升序列恰好为k的数的个数. 题目分析: 首先要理解\(o(nlogn)\)求LIS问题的思路,每次寻找第一个大于等于的数将其更改. 设dp[pos][s ...
- hdu4352 XHXJ's LIS[数位DP套状压DP+LIS$O(nlogn)$]
统计$[L,R]$内LIS长度为$k$的数的个数,$Q \le 10000,L,R < 2^{63}-1,k \le 10$. 首先肯定是数位DP.然后考虑怎么做这个dp.如果把$k$记录到状态 ...
- hdu4352 XHXJ's LIS(数位DP + LIS + 状态压缩)
#define xhxj (Xin Hang senior sister(学姐)) If you do not know xhxj, then carefully reading the entire ...
- hdu4352 XHXJ's LIS(数位dp)
题目传送门 XHXJ's LIS Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) ...
- HDU4352 XHXJ's LIS 题解 数位DP
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4352 题目大意: 求区间 \([L,R]\) 范围内最长上升子序列(Longest increasin ...
- Codeforces Round #235 (Div. 2) D. Roman and Numbers 状压dp+数位dp
题目链接: http://codeforces.com/problemset/problem/401/D D. Roman and Numbers time limit per test4 secon ...
- HDU 4336-Card Collector(状压,概率dp)
题意: 有n种卡片,每包面里面,可能有一张卡片或没有,已知每种卡片在面里出现的概率,求获得n种卡片,需要吃面的包数的期望 分析: n很小,用状压,以前做状压时做过这道题,但概率怎么推的不清楚,现在看来 ...
- CF1238E.Keyboard Purchase 题解 状压/子集划分DP
作者:zifeiy 标签:状压DP,子集划分DP 题目链接:https://codeforces.com/contest/1238/problem/E 题目大意: 给你一个长度为 \(n(n \le ...
- P4547 [THUWC2017]随机二分图(状压,期望DP)
期望好题. 发现 \(n\) 非常小,应该要想到状压的. 我们可以先只考虑 0 操作. 最难的还是状态: 我们用 \(S\) 表示左部点有哪些点已经有对应点, \(T\) 表示右部点有哪些点已经有对应 ...
随机推荐
- 云栖PPT下载 | 开源界大咖集体现身,开源数据库专场重点再回眸!
阿里云开源数据库项目最新发布 阿里巴巴集团副总裁.阿里云智能数据库事业部总裁.高级研究员李飞飞(飞刀).阿里云数据库资深技术专家楼方鑫(黄忠)以及阿里云数据库技术专家傅宇(齐木)三位阿里云技术专家为大 ...
- Shiro学习(9)JSP标签
Shiro提供了JSTL标签用于在JSP/GSP页面进行权限控制,如根据登录用户显示相应的页面按钮. 导入标签库 Java代码 <%@taglib prefix="shiro&qu ...
- ES数据导入导出
ES数据导入导出 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 ...
- 使用并行ssh提高工作效率
我们经常需要ssh到多个主机上执行相同的命令,为了提高效率,我们通常会自己写个脚本,循环遍历执行我们的命令,比如: for host in `cat hosts.txt`;do ssh usernam ...
- 一些识别CMS的经验方法总结
今天学到了一些识别CMS的快速方法,也算是一种信息收集经验的积累,在这里要感谢一下我的同事“gakki的童养夫”对我的大力支持. 如何判断网站的CMS? robots.txt文件 robots.txt ...
- Git 学习第三天(二)
默认情况下, Git合并是采用"fast forward"模式,但这种模式下,如果删除分支,会丢掉分支信息 禁用 fast forward 模式: git merge --no-f ...
- CUDA编程入门笔记
1.线程块(block)是独立执行的,在执行的过程中线程块之间互不干扰,因此它们的执行顺序是随机的 2.同一线程块中的线程可以通过访问共享内存(shared memory)或者通过同步函数__sync ...
- 【一】Jmeter接口自动化测试系列之参数化方法
Jmeter作为虽然作为一款和LoadRunner相媲美的性能测试工具,但参数化功能实在不咋地,这里我大概总结了一下Jmeter的参数化方法! 至于参数化的用途,我这里就不多说了,做测试的都明白吧!本 ...
- [已解决]报错SyntaxError: Non-ASCII character '\xe6'
解决方案:开头加上 # -*- coding: utf-8 -*
- man bash
BASH(1) General Commands Manual BASH(1) NAME bash - GNU Bourne-Again SHell SYNOPSIS bash [options] [ ...
