杭电多校第一场-M-Code

题目描述

After returning with honour from ICPC(International Cat Programming Contest) World Finals, Tom decides to say goodbye to ICPC and start a new period of life. He quickly gets interested in AI.
In the subject of Machine Learning, there is a classical classification model called perceptron, defined as follows:
Assuming we get a set of training samples: D={(x1,y1),(x2,y2),...,(xN,yN)}, with their inputs x∈Rd, and outputs y∈{−1,1}. We will try to find a function 
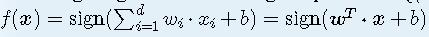 so that f(xi)=yi,i=1,2,...,N.
w,x mentioned above are all d-dimensional vectors, i.e. w=(w1,w2,...,wd), x=(x1,x2,...,xd). To simplify the question, let w0=b, x0=1, then 

Therefore, finding a satisfying function f(x) is equivalent to finding a proper w.
To solve the problem, we have a algorithm, PLA(Popcorn Label Algorithm).
Accoding to PLA, we will randomly generate w.
If f(x)=sign(wT⋅x) fails to give 
any element (xi,yi)∈D the right classification, i.e. f(xi)≠yi, then we will replace w with another random vector. We will do this repeatedly until all the samples ∈D are correctly classified.
As a former-JBer, Tom excels in programming and quickly wrote the pseudocode of PLA.
w := a random vector
while true do
    flag:=true
    for i:=1 to N do
        if f(x[ i ]) != y[ i ] then
            flag:=false
            break
    if flag then
        break
    else
        w := a random vector
return w
But Tom found that, in some occasions, PLA will end up into an infinite loop, which confuses him a lot. You are required to help Tom determine, when performed on a given sample set D, if PLA will end up into an infinite loop. Print Infinite loop! if so, or Successful! otherwise.
We only consider cases when d=2 for simplification.

输入

The first line contains an integer T(1≤T≤1000), the number of test cases.
Each test case begins with a line containing a single integer n(1≤n≤100), size of the set of training samples D.
Then n lines follow, the ith of which contains three integers xi,1,xi,2,yi (−105≤xi,1,xi,2≤105, yi∈{−1,1}), indicating the ith sample (xi,yi) in D, where xi=(xi,1,xi,2).

输出

For each test case, output a single line containing the answer: “Infinite loop!” or “Successful!”.

题意是给你n个三元组(x1,x2,y)，问你是否存在a,b,c使得对所有的三元组满足sgn(ax1+bx2+c)=y;

官方题解:
d= 时，f(x) =sgn(ax1+bx2+c)，f(x) =  对应于二维平面上的一条直线，直线一侧的点取值为 ，直线另一侧的取值为 -。
故该问题等价于能否找到一条直线将平面上的两类点分开，等价于判断这两类点分别组成的两个凸包是否相交。

判断凸包是否相交，参考https://www.cnblogs.com/ITUPC/p/5987593.html

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const double eps=1e-;
const int N=;
int sgn(double x)
{
    if (fabs(x)<eps)return ;
    if (x<)return -;
    else return ;
}
struct Point {
    ll x,y;
    Point() {}
    Point(ll _x,ll _y)
    {
        x=_x; y=_y;
    }
    Point operator -(const Point &b)
    {
        return Point(x-b.x,y-b.y);
    }
    ll operator ^(const Point &b)
    {
        return x*b.y-y*b.x;
    }
    ll operator *(const Point &b)
    {
        return x*b.x+y*b.y;
    }
    bool operator<(const Point &b)const
    {
        if(fabs(y-b.y)<eps) return x<b.x;
        return y<b.y;
    }
};
double Length(Point A)
{
    return sqrt(A*A);
}
double Angle(Point A,Point B)
{
    return acos((A*B)/Length(A)/Length(B));
}
bool Inter(Point a1,Point a2,Point b1,Point b2)
{
    ll c1=(a2-a1)^(b1-a1),c2=(a2-a1)^(b2-a1),c3=(b2-b1)^(a1-b1),c4=(b2-b1)^(a2-b1);
    return sgn(c1)*sgn(c2)<&&sgn(c3)*sgn(c4)<;
}

int Graham(Point p[],int n,Point q[])
{
     int top=;
     sort(p,p+n);
     if (n==) return ;
     q[]=p[];
     if (n==) return ;
     q[]=p[];
     if (n==) return ;
     q[]=p[];
     for (int i=;i<n;i++)
    {
         while(top&&((q[top]-q[top-])^(p[i]-q[top-]))<=) top--;
         q[++top]=p[i];
     }
     int len=top;
     q[++top]=p[n-];
     for (int i=n-;i>=;i--)
     {
         while (top!=len&&((q[top]-q[top-])^(p[i]-q[top-]))<=) top--;
         q[++top]=p[i];
     }
     return top;
}

bool C_S(Point ch1[],int t1,Point ch2[],int t2)
{
    if (t1==) return ;
    double angle[],x;
    int i,j,k;
    if (t1==)
    {
        for(i=;i<t2;i++)
        {
            k=sgn((ch1[]-ch1[])^(ch2[i]-ch1[]));
            if (k== && (ch1[]-ch1[])*(ch2[i]-ch1[])>)
            {
                if (Length(ch2[i]-ch1[])<Length(ch1[]-ch1[])) break;
            }
        }
        if (i<t2) return ;
        if (t2== && Inter(ch1[],ch1[],ch2[],ch2[])) return ;
        return ;
    }
    angle[]=;
    for (int i=;i<t1;i++) angle[i-]=Angle(ch1[]-ch1[],ch1[i]-ch1[]);
    for (i=;i<t2;i++)
    {
        j=sgn((ch1[]-ch1[])^(ch2[i]-ch1[]));
        if (j< || (j== && (ch1[]-ch1[])*(ch2[i]-ch1[])<)) continue;
        j=sgn((ch1[t1-]-ch1[])^(ch2[i]-ch1[]));
        if (j> || (j== && (ch1[t1-]-ch1[])*(ch2[i]-ch1[])<)) continue;
        x=Angle(ch1[]-ch1[],ch2[i]-ch1[]);
        int m=lower_bound(angle,angle+t1-,x)-angle;
        if (m==) j=; else j=m-;
        k=sgn((ch1[j+]-ch2[i])^(ch1[j+]-ch2[i]));
        if (k>=) break;
    }
    if (i<t2) return ;
    return ;
}
Point p1[N],p2[N],ch1[N],ch2[N];
int T,n;
int main()
{
    //freopen("1.in","r",stdin);
    //freopen("1.out","w",stdout);
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        int cnt1=,cnt2=;
        ll x,y; int z;
        for(int i=;i<n;i++)
        {
            scanf("%lld%lld%d",&x,&y,&z);
            if (z==) p1[cnt1++]=Point(x,y);
            else p2[cnt2++]=Point(x,y);
        }
        int t1=Graham(p1,cnt1,ch1);
        int t2=Graham(p2,cnt2,ch2);
        if (C_S(ch1,t1,ch2,t2)&&C_S(ch2,t2,ch1,t1)) printf("Successful!\n");
        else printf("Infinite loop!\n");
    }
    //fclose(stdin);
    //fclose(stdout);
    return ;
}