集中式大规模MIMO

同一小区的所有接入点( access point，AP) 布置在同一个基站( base station，BS) 中，并且 AP 之间的间距非常小，这种布置方式称为集中式大规模MIMO。

集中式结构虽然可以有效解决回程线路上的资源消耗问题，但是在用户的覆盖率，尤其在小区边缘用户的覆盖率上，还存在着许多不足之处 

无小区大规模MIMO

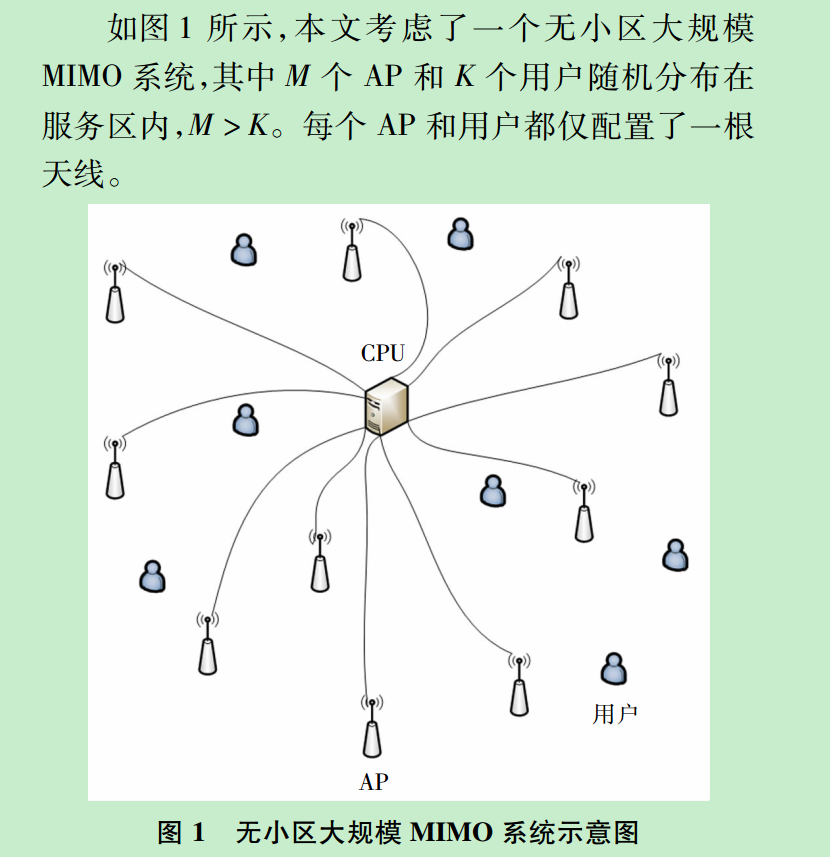
同传统的小区通信相比，无小区大规模 MIMO 取消了小区之间的划分，AP 的部署方式也变成了分布式。所有 AP 通过无差错的光纤网络与中央处理器( central processing unit，CPU) 进行通信。当有用户请求服务时，分布在服务区内的所有 AP 都为其提供服务。这种 AP 无处不在的服务方式可以提供极高的宏增益以及覆盖率，因此在工业和学术界得到了广泛的研究。

小小知识点（三十）集中式大规模和无小区大规模MIMO的更多相关文章

  1. 小小知识点（十八）U盘中病毒了，System Volume Information文件夹删除不掉

    win+R调出命令窗口后搜索cmd,启用cmd命令编辑器,并输入以下命令: attrib "H:\System Volume Information" -s   //这句话可以选择 ...

  2. 小小知识点（十五）——origin pro 2018 安装和消除demo字样

    安装 1.安装过成中选择语言为中文或者英文,安装完成后可在注册表中切换语言. 2.安装过程中使用序列号 中文版:DF2W8-9089-7991320英文版:GF3S4-9089-7991320 3.安 ...

  3. 小小知识点（十四）——Adobe photoshop cc 2018中简单抠图的一些基本操作

    一 如何抠图 1. 右键弹出选择工具,随后鼠标左键选择快速选择工具 2.通过点击鼠标,选择想要的区域: Alt+鼠标右键  左右拖动鼠标可调整画笔大小 Alt+鼠标滑轮,可放大或缩小画布大小 ctrl ...

  4. git-版本管理工具的介绍+发展史+分布式版本控制系统和集中式版本控制系统的区别

    一.版本管理工具的介绍: 1.备份文件: 2.记录历史: 3.多端共享: 4.团队协作: 二.版本管理工具的发展史: 1.cvs: 集中式   1985: 2.svn:  集中式    2000: 3 ...

  5. 通过Dapr实现一个简单的基于.net的微服务电商系统(十五)——集中式接口文档实现

    之前有小伙伴在评论区留言说如何集成swagger,最开始没有想透给了对方一个似是而非的回答.实际上后来下来想了一下,用.NET5 提供的Source Generator其实可以很方便的实现接口集成.今 ...

  6. 第三十六个知识点：Index Calculus算法

    第三十六个知识点:Index Calculus算法 我们这篇博客继续描述一种数学攻击,这种数学攻击被叫做Index Calculus(IC)算法. 注意这里Index Calculus算法没有找到合适 ...

  7. 精选Spring Boot三十五道必知必会知识点

    Spring Boot 是微服务中最好的 Java 框架. 我们建议你能够成为一名 Spring Boot 的专家.本文精选了三十五个常见的Spring Boot知识点,祝你一臂之力! 问题一 Spr ...

  8. centos LB负载均衡集群 三种模式区别 LVS/NAT 配置 LVS/DR 配置 LVS/DR + keepalived配置 nginx ip_hash 实现长连接 LVS是四层LB 注意down掉网卡的方法 nginx效率没有LVS高 ipvsadm命令集 测试LVS方法 第三十三节课

    centos   LB负载均衡集群 三种模式区别 LVS/NAT 配置  LVS/DR 配置  LVS/DR + keepalived配置  nginx ip_hash 实现长连接  LVS是四层LB ...

  9. 第三十四个知识点：描述攻击离散对数问题的baby-step/Giant-step方法

    第三十四个知识点:描述攻击离散对数问题的baby-step/Giant-step方法 Baby-step/Giant-step是Dnaiel Shanks为解决DLP问题开发的算法.DLP问题已经是许 ...

随机推荐

  1. javascript 容易混淆遗忘的基础知识

    1.  标识符     所谓标识符,就是指变量.函数.属性的名字,或者函数的参数.标识符可以是按照下列格式规则组合起来的一或多个字符:     1.1   第一个字符必须是一个字母.下划线( _ )或 ...

  2. hdu 1535 Invitation Cards（spfa）

    Invitation Cards Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others ...

  3. Python--day40--datetime,socketserver,Threading模块分别是哪些模块的高层模块

  4. C# GUID ToString

    最近在看到小伙伴直接使用 Guid.ToString ,我告诉他需要使用 Guid.ToString("N") ,为什么需要使用 N ,因为默认的是 D 会出现连字符. Guid ...

  5. 【u228】圣诞树

    [问题描述] 圣诞特别礼物挂在一棵圣诞树上,这棵树有n层,每层有一件礼物,每件礼物都有一个价值,有的礼物还有一些连结线,与下层的礼物相连,领取礼物的规则如下:任选一件礼物,它的下面如果有连结线,则可以 ...

  6. window 系统下修改`CMD`的编码格式的方法，`CHCP` 的 使用

    CHCP的使用 CHCP是一个计算机指令,能够显示或设置活动代码页编号. 一般上是在命令提示框中使用,用来查询和修改命令提示框的编码格式 具体使用方法 查看活动代码页编号 方式1: >>& ...

  7. 获取 Nuget 版本号

    本文告诉大家通过命令行获取 Nuget 的版本号 在 Nuget 中没有 -version 和 -v 和 --version 等写法,只需要直接输入 nuget 在第一行就会显示版本号 nuget N ...

  8. java 菜单

    继承体系 MenuBar,Menu,MenuItem之间的关系: 先创建菜单条,再创建菜单,每一个菜单中建立菜单项. 也可以菜单添加到菜单中,作为子菜单. 通过setMenuBar()方法,将菜单添加 ...

  9. linux 位操作

    atomic_t 类型在进行整数算术时是不错的. 但是, 它无法工作的好, 当你需要以原子方 式操作单个位时. 为此, 内核提供了一套函数来原子地修改或测试单个位. 因为整个操作 在单步内发生, 没有 ...

  10. 关于对height:100%的研究

    参考此链接: https://segmentfault.com/a/1190000012707337