【笔记】机器学习 - 李宏毅 - 6 - Logistic Regression

Logistic Regression 逻辑回归

逻辑回归与线性回归有很多相似的地方。后面会做对比，先将逻辑回归函数可视化一下。

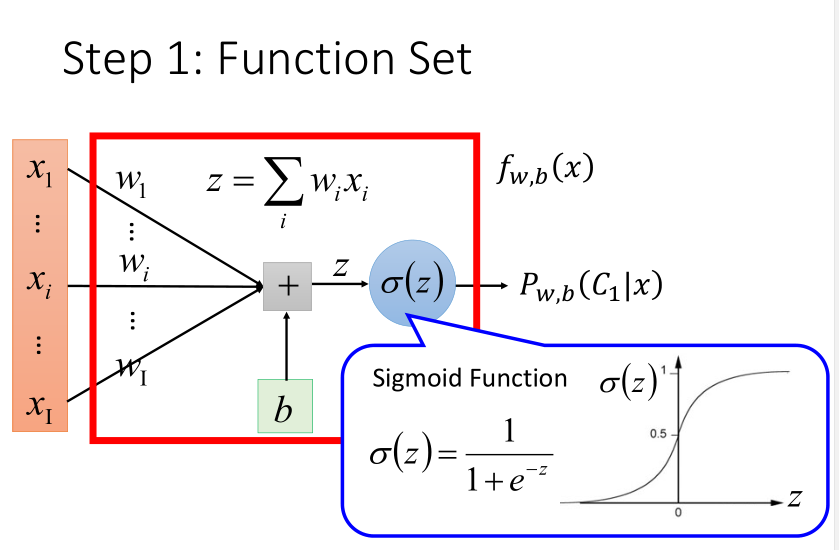
与其所对应的损失函数如下，并将求max转换为min，并转换为求指数形式，便于计算。

最后得到的是两个伯努利分布（function output & target）的交叉熵（两个分布的接近程度，如果分布相同，则交叉熵为0）。

经过求导，最后得到的损失函数的偏导数和线性回归的是形式一致的。将其三个步骤的对比归纳如下。

为何用交叉熵而不用平方差，因为逻辑回归模型在求导过程中，没有命中target导数也为0，得到的结果不正确。而且即使不为0，因为微分值小，也会导致迭代速度很慢。

逻辑回归的方法称为Discriminative（判别） 方法；上一篇中用高斯来描述后验概率，称为 Generative（生成） 方法。他们的函数集都是一样的，只是描述方式不同。

如果是逻辑回归，就可以直接用梯度下降法找出w和b；如果是概率生成模型，像上篇那样求出 \(μ^1, μ^2\)，协方差矩阵的逆，然后就能算出w和b。

因为中间经过的步骤不同，所以最后得到的结果准确率也有所区别。

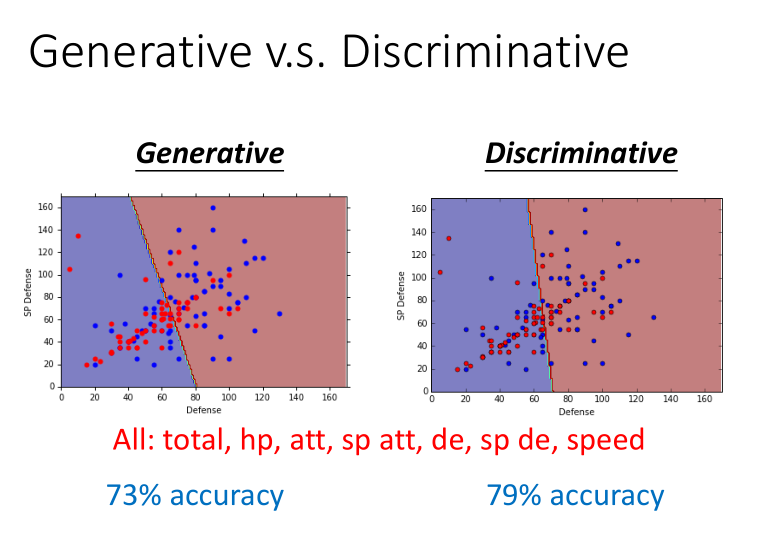
下面这个例子说明，用贝叶斯方法在计算概率的时候，机器“脑补”了数据量不足所掩盖的可能性。

判别比生成好吗？生成方法相比于判别方法，需要的训练数据量更小，鲁棒性更好，先验和类相关的概率可以从不同的来源计算。
比如语音识别中计算先验概率，用的生成方法，并不全是DNN。

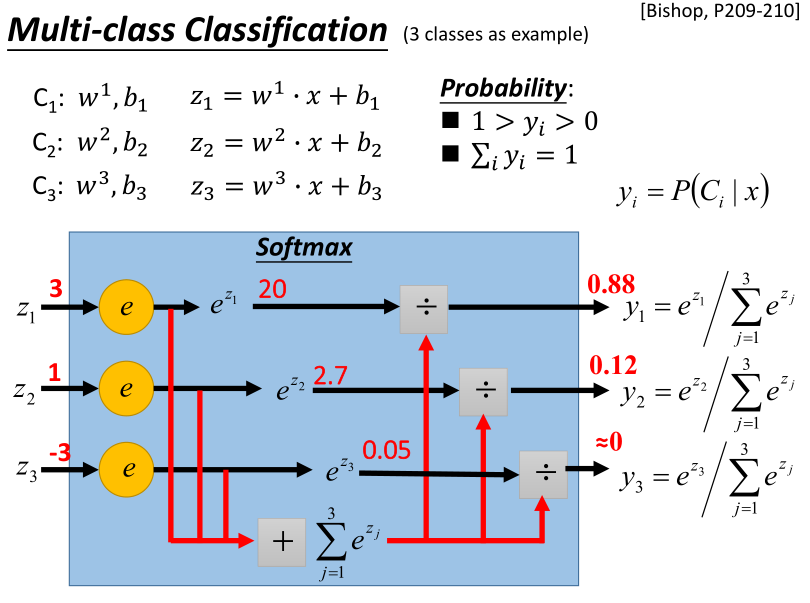
多分类问题

Softmax是进行exponential（指数化），将exponential 的结果相加，再分别用 exponential 的结果除以相加的结果。
原本\(z_1,z_2,z_3\)可以是任何值，但做完Softmax之后输出会被限制住，都介于0到1之间，并且和是1。Softmax就是对最大值进行强化。
指数簇分布的最大熵等价于其指数形式的最大似然界，应用如二项式的sigmoid, 多项式的softmax。

\(\hat{y}\)也定义成矩阵形式，计算交叉熵。

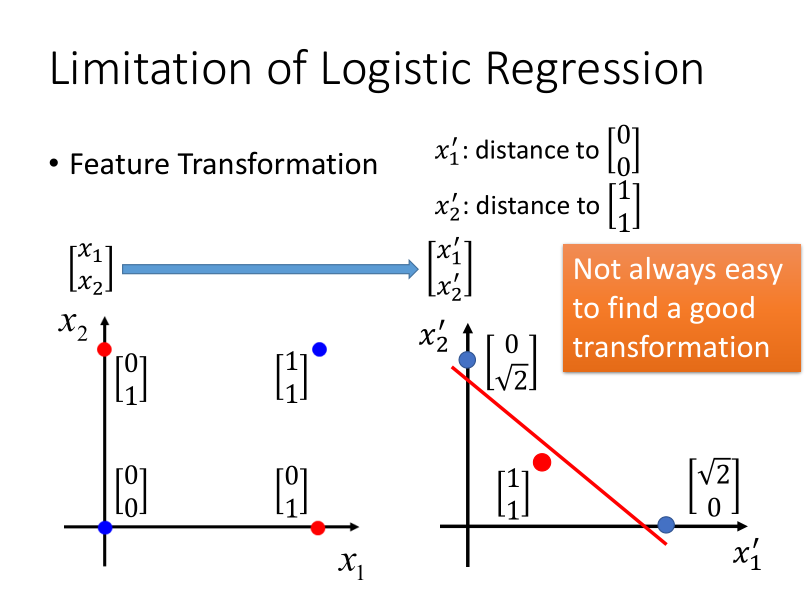
如果说两个类别分布在两个对角线的两端，则需要先进行特征转换，多加一层操作，深度学习的神经网络就是类似这样的多层操作。