[洛谷P4012] [网络流24题] 深海机器人问题

Description###

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。

潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。

深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。

每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。

本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。

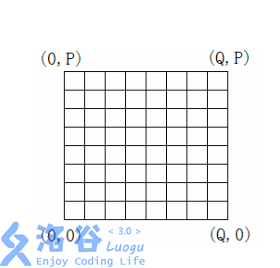
用一个 P×Q 网格表示深海机器人的可移动位置。西南角的坐标为(0,0) ，东北角的坐标为(Q,P) 。

给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。

计算深海机器人的最优移动方案， 使深海机器人到达目的地后，采集到的生物标本的总价值最高。

Input###

文件的第 11 行为深海机器人的出发位置数 a ,和目的地数 b 。

第 22 行为 P 和 Q 的值。

接下来的 P+1 行,每行有 Q 个正整数,表示向东移动路径上生物标本的价值,行数据依从南到北方向排列。

再接下来的 Q+1 行,每行有 P 个正整数,表示向北移动路径上生物标本的价值,行数据依从西到东方向排列。

接下来的 a 行,每行有 3 个正整数 k,x,y ,表示有 k 个深海机器人从 (x,y) 位置坐标出发。

再接下来的 b 行,每行有 3 个正整数 r,x,y ,表示有 r 个深海机器人可选择 (x,y) 位置坐标作为目的地。

a行和b行输入时横纵坐标要反过来

Output###

输出采集到的生物标本的最高总价值.

Sample Input###

1 1

2 2

1 2

3 4

5 6

7 2

8 10

9 3

2 0 0

2 2 2

Sample Output###

42

HINT###

1≤P,Q≤15

1≤a≤4

1≤b≤6

---

想法##

还是挺容易的一道题

直接按题目所说的建图，每相邻两个点间连两条边

一条容量为1，代价为-val

另一条容量为INF，代价为0

跑一遍最小费用最大流，答案\(\times\)-1就行了

---

代码##

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>

#define INF 2000000000

using namespace std;

typedef long long ll;
const int N = 17;
const int M = N*N;

struct node{
    int v,f,c;
    node *next,*rev;
}pool[M*8+20],*h[M],*pree[M];
int cnt;

void addedge(int u,int v,int f,int c){
    node *p=&pool[++cnt],*q=&pool[++cnt];
    p->v=v;p->next=h[u];h[u]=p; p->f=f;p->c=c;p->rev=q;
    q->v=u;q->next=h[v];h[v]=q; q->f=0;q->c=-c;q->rev=p;
}

int S,T;
ll d[M];
int vis[M],pre[M];
queue<int> que;
bool spfa(){
    int u,v;
    while(!que.empty()) que.pop();
    for(int i=S;i<=T;i++) d[i]=INF;
    d[S]=0; vis[S]=1;
    que.push(S);
    while(!que.empty()){
        u=que.front(); que.pop();
        vis[u]=0;
        for(node *p=h[u];p;p=p->next)
            if(p->f && d[v=p->v]>d[u]+p->c){
                d[v]=d[u]+p->c;
                pre[v]=u;
                pree[v]=p;
                if(!vis[v]) { que.push(v); vis[v]=1; }
            }
    }
    return d[T]!=INF;
}
void cal(ll &f,ll &c){
    int u=T,w=INF;
    node *p=pree[u];
    while(u!=S){
        w=min(w,p->f);
        u=pre[u]; p=pree[u];
    }
    f+=w; c+=w*d[T];
    u=T; p=pree[u];
    while(u!=S){
        p->f-=w;
        p->rev->f+=w;
        u=pre[u]; p=pree[u];
    }
}
ll MCMF(){
    ll f=0,c=0;
    while(spfa()) cal(f,c);
    return c;
}

int a,b,n,m;

int main()
{
    scanf("%d%d%d%d",&a,&b,&n,&m);
    n++;m++;
    S=0; T=n*m+1;

    int x,y,k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<m;j++) {
            scanf("%d",&x);
            addedge((i-1)*m+j,(i-1)*m+j+1,1,-x);
            addedge((i-1)*m+j,(i-1)*m+j+1,INF,0);
        }
    for(int j=1;j<=m;j++)
        for(int i=1;i<n;i++) {
            scanf("%d",&x);
            addedge((i-1)*m+j,i*m+j,1,-x);
            addedge((i-1)*m+j,i*m+j,INF,0);
        }
    for(int i=0;i<a;i++){
        scanf("%d%d%d",&k,&x,&y);
        x++;y++;
        addedge(S,(x-1)*m+y,k,0);
    }
    for(int i=0;i<b;i++){
        scanf("%d%d%d",&k,&x,&y);
        x++;y++;
        addedge((x-1)*m+y,T,k,0);
    }

    printf("%lld\n",-MCMF());

    return 0;
}