TopCoder[SRM587 DIV 1]:ThreeColorability(900)
Problem Statement |
|||||||||||||
|
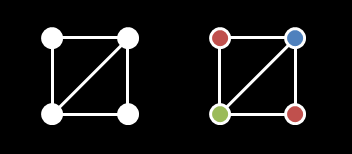
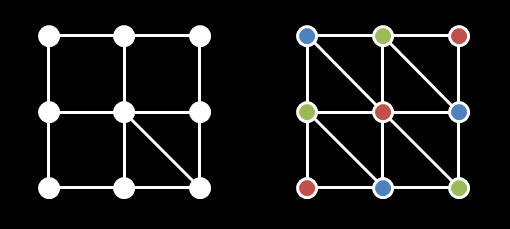
There is a H times W rectangle divided into unit cells. The rows of cells are numbered 0 to H-1 from top to bottom, and the columns are numbered 0 to W-1 from left to right. The corners of cells are called lattice points. By definition, there are (H+1)*(W+1) lattice points in our rectangle. Each of the four edges of each cell is painted white. Additionally, in some cells exactly one of the two diagonals is painted white. In the remaining cells no diagonal is painted white yet. Later, you are going to paint exactly one of the diagonals white in each of these cells. Once you are done painting the diagonals, your next goal will be to color each of the lattice points using one of three available colors: red, green, or blue. There is only one constraint: adjacent lattice points are not allowed to share the same color. Two lattice points are called adjacent if they are connected by a white line segment. (In other words, consecutive corners of a cell are always adjacent, opposite corners of a cell are adjacent if and only if they are connected by a painted diagonal, and no other pairs of lattice points are adjacent.) Obviously, you need to paint the missing diagonals in such a way that there will be a valid coloring of lattice points, if possible. You are given a vector <string> cells with H elements, each consisting of W characters. If cells[i][j] is 'N', there is a diagonal line from the top left to the bottom right corner in the cell in row i, column j. If cells[i][j] is 'Z', there is a diagonal line from the top right to the bottom left corner in the cell in row i, column j. If cells[i][j] is '?', there is no diagonal yet in the cell in row i, column j. If it is impossible to fill in the missing diagonals in such a way that there will be a valid coloring of all lattice points, return an empty vector <string>. Otherwise, return a vector <string> that represents the rectangle with all the missing diagonals filled in. I.e., the return value must be obtained from cells by replacing each '?' by either 'N' or 'Z'. The return value must represent a rectangle for which a valid coloring of its lattice points exists. If there are multiple possibilities, return the lexicographically smallest one. |
|||||||||||||
Definition |
|||||||||||||
|
|||||||||||||
Limits |
|||||||||||||
|
|||||||||||||
Notes |
|||||||||||||
| - | Given two different vector <string>s A and B with the same number of elements, find the smallest index i such that A[i] and B[i] differ. If A[i] < B[i] we say that A is lexicographically smaller than B and vice versa. | ||||||||||||
Constraints |
|||||||||||||
| - | cells will contain between 1 and 50 elements, inclusive. | ||||||||||||
| - | Each element of cells will contain between 1 and 50 characters, inclusive. | ||||||||||||
| - | All elements of cells will contain the same number of characters. | ||||||||||||
| - | Each character of cells will be either 'N' or 'Z' or '?'. | ||||||||||||
Examples |
|||||||||||||
| 0) | |||||||||||||
|
|||||||||||||
| 1) | |||||||||||||
|
|||||||||||||
| 2) | |||||||||||||
|
|||||||||||||
| 3) | |||||||||||||
|
|||||||||||||
| 4) | |||||||||||||
|
|||||||||||||
题意:给定一个网格图,为每个格子安排对角线(有些格子已经安排好),使得新图可以被用三种颜色染色(被一条边相连的两个点不能染同一种颜色)。两种对角线用'Z'与'N'表示。
题解:
画图找规律,可以发现,在相邻的四个格子中(即3*3的格点),'Z'的数量为偶数。
由此可以推得,在一个合法的图中,一行格子的对角线安排如果不与相邻的行完全相同,就与相邻的行完全相反。
即不管在哪一行,第i列与第j列格子对角线安排是否相同的关系都是一样的。
即我们可以用已知的每一行内的关系,通过并查集处理出第一行各格子的关系。
然后在满足原本安排方案的情况下,求出一种字典序最小的安排方案。
代码:
int fa[],a[][],n,m;
int getf(int x)
{
if(fa[x]!=x)fa[x]=getf(fa[x]);
return fa[x];
}
int hb(int xx,int yy)
{
int x=getf(xx),y=getf(xx+m),z=getf(yy),w=getf(yy+m);
if((x==w)or(y==z))return ;
fa[x]=z; fa[y]=w; return ;
}
int qf(int xx,int yy)
{
int x=getf(xx),y=getf(xx+m),z=getf(yy),w=getf(yy+m);
if((x==z)or(y==w))return ;
fa[x]=w; fa[y]=z; return ;
}
int pd(char x)
{ if(x=='N')return ; if(x=='Z')return -; return ; }
class ThreeColorability
{
public:
vector <string> lexSmallest(vector <string> cells)
{
//$CARETPOSITION$
vector<string>ans;
n=cells.size(); m=cells[].size();
for(int i=;i<m;i++)fa[i]=i,fa[i+m]=i+m;
for(int i=;i<n;i++)
for(int j=;j<m-;j++)
if(cells[i][j]!='?')
{
for(int k=j+;k<m;k++)
if(cells[i][k]!='?')
{
int flag;
if(cells[i][j]==cells[i][k])flag=hb(j,k);else flag=qf(j,k);
if(flag==)return ans;
}
}
for(int j=;j<m;j++)
{
int t=pd(cells[][j]);
if(t!=)
{
int x=getf(j),y=getf(j+m);
for(int k=;k<m;k++)
{
if(getf(k)==x)a[][k]=t;else
if(getf(k)==y)a[][k]=-t;
}
}
}
for(int j=;j<m;j++)
if(a[][j]==)
{
int x=getf(j),y=getf(j+m);
for(int k=;k<m;k++)
{
if(getf(k)==x)a[][k]=;else
if(getf(k)==y)a[][k]=-;
}
}
for(int i=;i<n;i++)
{
int x=;
for(int j=;j<m;j++)if(pd(cells[i][j])!=)
{ if(pd(cells[i][j])==a[i-][j])x=;else x=-; break; }
if(x==){ if(a[i-][]==)x=;else x=-; }
for(int j=;j<m;j++)a[i][j]=a[i-][j]*x;
}
for(int i=;i<n;i++)
{
string s; s.clear();
for(int j=;j<m;j++)if(a[i][j]==)s=s+'N';else s=s+'Z';
ans.push_back(s);
}
return ans;
}
};
TopCoder[SRM587 DIV 1]:ThreeColorability(900)的更多相关文章
- TopCoder[SRM587 DIV 1]:TriangleXor(550)
Problem Statement You are given an int W. There is a rectangle in the XY-plane with corners at ...
- TopCoder SRM 559 Div 1 - Problem 900 CircusTents
传送门:https://284914869.github.io/AEoj/559.html 题目简述: n个实心圆,两两没有交集,在第一个圆上找一个点,使得它到另外一个圆上某个点的最短距离的最小值尽量 ...
- TopCoder[SRM513 DIV 1]:Reflections(1000)
Problem Statement Manao is playing a new game called Reflections. The goal of the game is trans ...
- Topcoder SRM584 DIV 2 500
#include <set> #include <iostream> #include <string> #include <vector> using ...
- Topcoder SRM583 DIV 2 250
#include <string> #include <iostream> using namespace std; class SwappingDigits { public ...
- 【补解体报告】topcoder 634 DIV 2
A:应该是道语文题,注意边界就好: B:开始考虑的太复杂,没能够完全提取题目的思维. 但还是A了!我愚蠢的做法:二分答案加暴力枚举, 枚举的时候是完全模拟的,比如每次取得时候都是从大到小的去取,最后统 ...
- Topcoder Srm627 DIV 2
A,B:很水,注意边界,话说HACK都是这些原因. C: R[I][J]:表示反转I-J能改变冒泡排序的次数: DP方程:dp[i][k]=max(dp[j][k],dp[j][k-1]+dp[j][ ...
- Topcoder SRM548 Div 1
1. KingdomAndTrees 给出n个数a[1..n],求一个数组b[1..n]满足b严格递增,且b[1]>=1. 定义代价为W = max{abs(a[i]-b[i])},求代价最小值 ...
- TopCoder SRM 701 Div2 Problem 900 ThueMorseGame(博弈+预处理)
题意 Alice和Bob在玩一个游戏,Alice先手. 每次一个人可以从一堆式子中拿走任意数量(不超过m)的式子. 取走最后一颗式子的人胜利. 当一个取完某一步的时候剩下的石子数量的二进制表示中1的 ...
随机推荐
- xshell本地上传文件到Ubuntu上及从Ubuntu上下载文件到本地
1.第一种方法是最常用的 :如果下载了Xshell和Xftp,Ctrl+Alt+F就可以选择文件的互传了!(虚拟机/云服务器通用)--只要相互间能ping得通. 2.第二种方法 :ubuntu环境下安 ...
- Scala(一)基础
OOP 面向对象编程 AOP 面向切面编程 FP 函数式编程 编程语言都要定义变量,一些代码是用来注释的,变量和变量之间有一些关系,要做一些运算,运算离不开流程控制,进行运算的数据往往来自数据结构,最 ...
- CentOS7.6 部署asp.net core2.2 应用
1.安装.net Core SDK 在安装.NET之前,您需要注册Microsoft密钥,注册产品存储库并安装所需的依赖项.这只需要每台机器完成一次. 打开终端并运行以下命令: sudo rpm -U ...
- APUE线程控制
一.线程的限制 sysconf可以查看的值 PTHREAD_DESTRUCTOR_ITERATIONS 线程退出时操作系统实现试图销毁线程特定数据的最大次数 _SC_THREAD_DESTRUCTOR ...
- 收集python2代码转python3遇到的问题
在程序中做python版本判断 sys.version_info # sys.version_info(major=2, minor=7, micro=16, releaselevel='final' ...
- App响应式布局
1.手机的响应式布局,所有的单位用rem来表示. 如:设计稿的宽度是750,则html标签的font-size=屏幕宽度/7.5.那么在网页中的尺寸 = 设计高上实际的尺寸/100. 把下面的代码作为 ...
- 第十四届华中科技大学程序设计竞赛--J Various Tree
链接:https://www.nowcoder.com/acm/contest/106/J来源:牛客网 时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 32768K,其他语言65536 ...
- 关于类中的参数类型和return返回值
基础有些忘了,现在重新巩固一下 先定义一个Person类 class Person(): def __init__(self,name,age,height): self.name=name, sel ...
- Java学习之classpath
要运行class文件,必须在class文件所在的目录下,那么是不是也可以通过设置系统变量来配置呢,当然有了classpath就来了 环境变量配置有两种 1.一劳永逸的 2.set 临时变量 我们用临时 ...
- Linux操作系统中对于NTFS读取目录功能的实现
1: /* 2: * We use the same basic approach as the old NTFS driver, i.e. we parse the 3: * index root ...