关于线段树的感悟(Segment Tree)

线段树的感悟 : 学过的东西一定要多回头看看,不然真的会忘个干干净净。

线段树的 Introduction :

English Name : Segment Tree
顾名思义 : 该数据结构由两个重要的东西组成 : 线段,树,连起来就是在树上的线段。
想一下,线段有啥特征 ?
不就是两个端点中间一条线吗，哈哈,也可以这么理解,但这样是不是稍微难听呀,所以
我们用一个华丽的词语来描述这个两点之间的一条线,这个词语就是不知道哪个先知发
明的，就是 -- 区间。
所以我们就可猜想到,所以线段树一定是用来处理区间问题的。

线段树长个啥样子？

展示一个区间  1 - 10 的一颗线段树,就是这么个树东西。

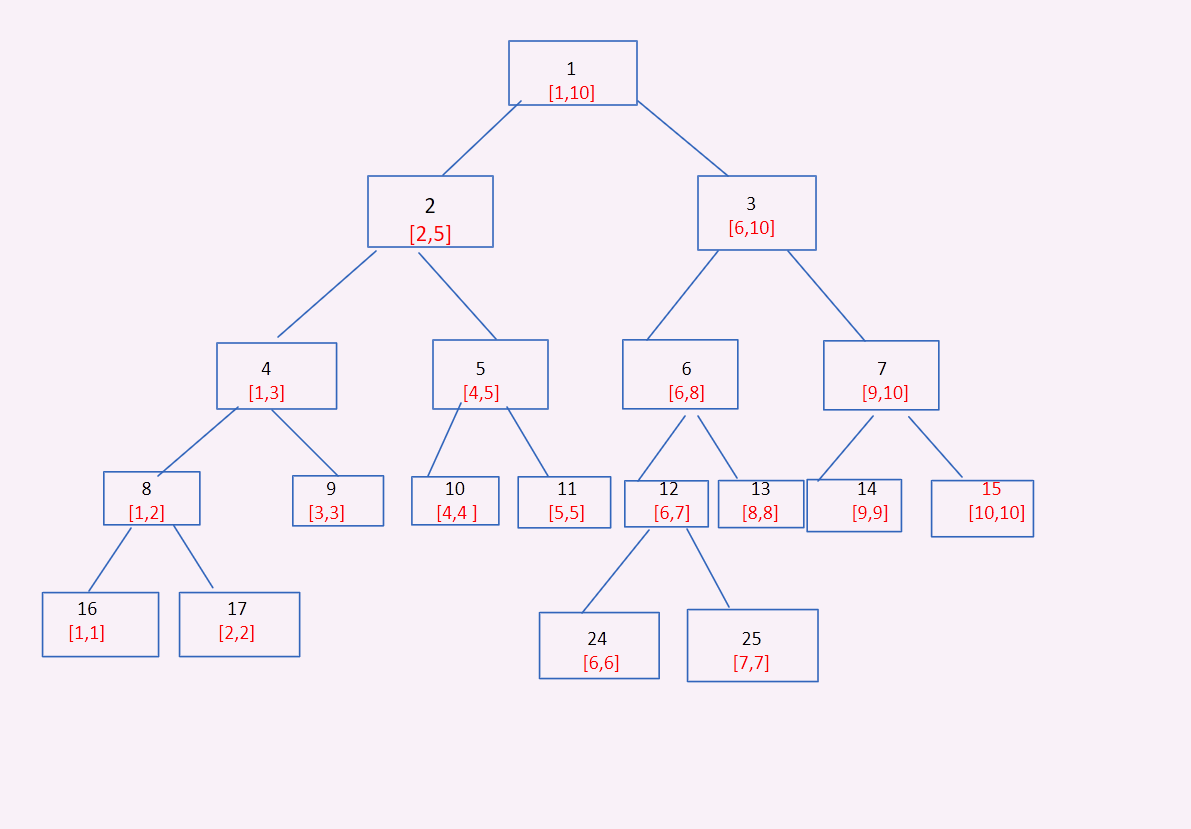
线段树的基本结构 :

1、线段树的每个节点都代表一个区间
2、线段树具有唯一的根节点,代表的区间的整个统计范围,[1,N]
3、线段树的每个叶节点都代表一个长度为 1 的元区间 [x,x],也就是我们原数组中每个值,原数组中有几个值
   就有多少个叶子节点(可以参照上图了解一下)。
4、对于每个内部节点 [l,r],它的左子节点是 [l,mid],右子节点是 [mid + 1，r],mid = l + r >> 1(向下取整)

线段树经常处理那些区间问题 ？

1、单点查询(查询某个位置上的值是多少)
2、单点修改(修改某个位置上的值)
3、区间查询(查询某个区间的 和、最大值、最小值、最大公约数、and so on)
4、区间修改(修改某个区间的值, eg：让某个区间都 + 一个数、and so on)

线段树需要注意的地方 :

1、结构体空间一定要开 4 倍,一定要记得看 4 倍(看上面这棵树,按节点编号我们可以看到一共有 25 个节点,但算上空余的位置呢?)
   会发现有 31 个节点,可以自己数一下,所以我们要开原数组的 4 倍,避免出现数组越界,非法访问的情况(段错误)。
2、区间判断的时候一定不要写反(下面写的时候就知道了,这个坑让我 Debug 了一个多小时)
3、没事多打打,模板,就当练手速了。

线段树的基本操作 :

1、Struct结构体存储

struct node {
	LL l,r;
	LL sum;  // 看需要向父节点传送什么
} tr[maxn << 2];

2、 Build

void pushup(LL u) {
	tr[u].sum = gcd(tr[u << 1].sum,tr[u << 1 | 1].sum);
	return ;
}

void build(LL u,LL l,LL r) {
	tr[u].l = l,tr[u].r = r;  // 初始化(节点 u 代表区间 [l,r])
	if(l == r) {
		tr[u].sum = b[l]; // 递归到叶节点赋初值
		return ;
	}
	LL mid = l + r >> 1;      // 折半
	build(u << 1,l,mid);      // 向左子节点递归
	build(u << 1 | 1,mid + 1,r); // 向右子节点递归
	pushup(u);                // 从下往上传递信息
	return;
}

3、Update

void update(LL u,LL x,LL v) {
	if(tr[u].l == tr[u].r) {        // 找到叶节点
		tr[u].sum += v;         // 在某个位置加上一个数
		return ;
	}
	LL mid = tr[u].l + tr[u].r >> 1;
	if(x <= mid) update(u << 1,x,v); // x 属于左半区间
	else update(u << 1 | 1,x,v);     // x 属于右半区间
	pushup(u);                       // 从下向上更新信息
	return ;
}

4、Query ：

1、若 [l,r] 完全覆盖了当前节点代表的区间,则立即回溯。
2、若左子节点与 [l,r] 有重叠部分,则递归访问左子节点。
3、若右子节点与 [l,r] 有重叠部分,则递归访问右子节点。

LL query(int u,int l,int r) {
    if(tr[u].l >= l && tr[u].r <= r) {   // 完全包含
        return tr[u].sum;
    }
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if(l <= mid) sum += query(u << 1,l,r);
    if(r > mid) sum += query(u << 1 | 1,l,r);
    return sum;
}

上述就是线段树的基本操作,基本上都是围绕单点问题进行操作,如果要涉及到复杂的区间操作，

例如 : 给区间 [l,r] 每个数都 + d

这时如果还用上述操作,我们就需要进行 l - r + 1 次操作,如果有多次这样的操作,显然时间

复杂度会很高,这时候我们应该选择什么样的方法来降低时间复杂度呢 ？

Lazy（懒） 标记应运而生

简单一点来说就是,减少重复的操作,如果说我们操作的每一个数都在一个区间范围内,那么
我们就可以直接处理这个区间,不需要再一个一个处理,比如上面的给区间的每一个数 + d;
假设说我们已经知道 [l,r] 完全包含一个区间 [x,y],也就是说 区间[x,y]是 [l,r]的
一个子区间,那么这个时候我们是不是直接可以计算出 [x,y] 这个区间 都 + d 后的值是
多少, (x - y + 1) * d（假设是求和的话）,这样我们就可以不再用去一个一个加,然后
再合并了,我们知道有这样的区间后,怎么用呢？这时候就需要进行标记一下,便于我们知道
这个地方有一个区间可以直接处理,不需要再麻烦着向下继续去处理了,是不是很懒,哈哈。

/*
    懒标记的含义 : 该节点曾经被修改,但其子节点尚未被更新。
    在后续的指令中,我们需要从某个节点向下递归时,检查该节点是否具有标记,若有标记,就根据
    标记信息更新 该节点 的两个子节点,同时为该节点的两个子节点增加标记,然后清楚 p 的标记。
*/
void pushdown(int u) {
    if(tr[u].lazy) {    // 节点 u 有标记
        tr[u << 1].sum += tr[u].lazy * (tr[u << 1].r - tr[u << 1].l + 1); // 更新左子节点信息
        tr[u << 1| 1].sum += tr[u].lazy * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1); // 更新右子节点
        tr[u << 1].lazy += tr[u].lazy;     // 给左子节点打延迟标记
        tr[u << 1 | 1].lazy += tr[u].lazy; // 给右子节点打延迟标记
        tr[u].lazy = 0;                    // 清楚父节点的延迟标记(这点很重要)
    }
    return ;
}

加上 Lazy 标记的其他操作 :

// Build 不变
// Update
void modify(int u,int l,int r,int x) {
    if(tr[u].l >= l && tr[u].r <= r) {  // 完全覆盖
        tr[u].sum += (tr[u].r- tr[u].l + 1) * x; // 更新节点信息
        tr[u].lazy += x;                // 给节点打延迟标记
        return ;
    }
    pushdown(u);                        // 下传延迟标记
    int mid = tr[u].l + tr[u].r >> 1;
    if(l <= mid) modify(u << 1,l,r,x);
    if(r > mid) modify(u << 1 | 1,l,r,x);
    pushup(u);
    return ;
}

// Query
LL query(int u,int l,int r) {
    if(tr[u].l >= l && tr[u].r <= r) {
        return tr[u].sum;
    }
    pushdown(u);                  // 同上
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if(l <= mid) sum += query(u << 1,l,r);
    if(r > mid) sum += query(u << 1 | 1,l,r);
    return sum;
}

总结 :

线段树的操作基本上就这些,哈哈,实际上自己就了解这么多,而且是最近有几场比赛碰见挺多的,就学了一下,
主要是手得多动动,有时候考察得还是比较复杂得,先把这些基础得模板搞懂吧。

例题(模板题)：

1、一个简单的整数问题

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1e5 + 10;
typedef long long LL;

struct node {
    int l,r;
    LL sum,lazy;
}tr[maxn << 2];
int a[maxn];
int n,m;
int l,r;

int main(void) {
    void build(int u,int l,int r);
    void modify(int u,int l,int r,int x);
    LL query(int u,int l,int r);
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= n; i ++) {
        scanf("%d",&a[i]);
    }
    build(1,1,n);
    while(m --) {
        char ch;
        cin >> ch;
        if(ch == 'Q') {
            scanf("%d",&l);
            printf("%lld\n",query(1,1,l) - query(1,1,l - 1));
        } else {
            int value;
            scanf("%d%d%d",&l,&r,&value);
            modify(1,l,r,value);
        }
    }
    return 0;
} 

void pushup(int u) {
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    return ;
}

void pushdown(int u) {
    if(tr[u].lazy) {
        tr[u << 1].sum += tr[u].lazy * (tr[u << 1].r - tr[u << 1].l + 1);
        tr[u << 1| 1].sum += tr[u].lazy * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1);
        tr[u << 1].lazy += tr[u].lazy;
        tr[u << 1 | 1].lazy += tr[u].lazy;
        tr[u].lazy = 0;
    }
    return ;
}

void build(int u,int l,int r) {
    tr[u].l = l,tr[u].r = r;
    if(l == r) {
        tr[u].sum = a[l];
        return ;
    }
    int mid = l + r >> 1;
    build(u << 1,l,mid);
    build(u << 1 | 1,mid + 1,r);
    pushup(u);
    return ;
}

void modify(int u,int l,int r,int x) {
    if(tr[u].l >= l && tr[u].r <= r) {
        tr[u].sum += (tr[u].r- tr[u].l + 1) * x;
        tr[u].lazy += x;
        return ;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if(l <= mid) modify(u << 1,l,r,x);
    if(r > mid) modify(u << 1 | 1,l,r,x);
    pushup(u);
    return ;
}

LL query(int u,int l,int r) {
    if(tr[u].l >= l && tr[u].r <= r) {
        return tr[u].sum;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if(l <= mid) sum += query(u << 1,l,r);
    if(r > mid) sum += query(u << 1 | 1,l,r);
    return sum;
}

2、一个简单的整数问题2

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1e5 + 10;
typedef long long LL;

struct node {
    int l,r;
    LL sum,lazy;
}tr[maxn << 2];
int a[maxn];
int n,m;
int l,r;

int main(void) {
    void build(int u,int l,int r);
    void modify(int u,int l,int r,int x);
    LL query(int u,int l,int r);
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= n; i ++) {
        scanf("%d",&a[i]);
    }
    build(1,1,n);
    while(m --) {
        char ch;
        cin >> ch;
        if(ch == 'Q') {
            scanf("%d%d",&l,&r);
            printf("%lld\n",query(1,l,r) );
        } else {
            int value;
            scanf("%d%d%d",&l,&r,&value);
            modify(1,l,r,value);
        }
    }
    return 0;
} 

void pushup(int u) {
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    return ;
}

void pushdown(int u) {
    if(tr[u].lazy) {
        tr[u << 1].sum += tr[u].lazy * (tr[u << 1].r - tr[u << 1].l + 1);
        tr[u << 1| 1].sum += tr[u].lazy * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1);
        tr[u << 1].lazy += tr[u].lazy;
        tr[u << 1 | 1].lazy += tr[u].lazy;
        tr[u].lazy = 0;
    }
    return ;
}

void build(int u,int l,int r) {
    tr[u].l = l,tr[u].r = r;
    if(l == r) {
        tr[u].sum = a[l];
        return ;
    }
    int mid = l + r >> 1;
    build(u << 1,l,mid);
    build(u << 1 | 1,mid + 1,r);
    pushup(u);
    return ;
}

void modify(int u,int l,int r,int x) {
    if(tr[u].l >= l && tr[u].r <= r) {
        tr[u].sum += (tr[u].r- tr[u].l + 1) * x;
        tr[u].lazy += x;
        return ;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if(l <= mid) modify(u << 1,l,r,x);
    if(r > mid) modify(u << 1 | 1,l,r,x);
    pushup(u);
    return ;
}

LL query(int u,int l,int r) {
    if(tr[u].l >= l && tr[u].r <= r) {
        return tr[u].sum;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if(l <= mid) sum += query(u << 1,l,r);
    if(r > mid) sum += query(u << 1 | 1,l,r);
    return sum;
}