bzoj 2038 A-小Z的袜子[hose] - 莫队算法

　　作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……
　　具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。

Input

输入文件第一行包含两个正整数N和M。N为袜子的数量，M为小Z所提的询问的数量。接下来一行包含N个正整数Ci，其中Ci表示第i只袜子的颜色，相同的颜色用相同的数字表示。再接下来M行，每行两个正整数L，R表示一个询问。

Output

包含M行，对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1，否则输出的A/B必须为最简分数。（详见样例）

Sample Input

6 4
1 2 3 3 3 2
2 6
1 3
3 5
1 6

Sample Output

2/5
0/1
1/1
4/15
【样例解释】
询问1：共C(5,2)=10种可能，其中抽出两个2有1种可能，抽出两个3有3种可能，概率为(1+3)/10=4/10=2/5。
询问2：共C(3,2)=3种可能，无法抽到颜色相同的袜子，概率为0/3=0/1。
询问3：共C(3,2)=3种可能，均为抽出两个3，概率为3/3=1/1。
注：上述C(a, b)表示组合数，组合数C(a, b)等价于在a个不同的物品中选取b个的选取方案数。
【数据规模和约定】
30%的数据中 N,M ≤ 5000；
60%的数据中 N,M ≤ 25000；
100%的数据中 N,M ≤ 50000，1 ≤ L < R ≤ N，Ci ≤ N。

---

　　这个是支持离线的一道题，那么可以试试用莫队算法。

　　那么看能不能在已知一个区间[l, r]的情况下，快速知道[l - 1, r],[l +１, r],[l, r - 1]和[l, r + 1]。这列主要最难(其实也不难)找的是方案数。那么来看，如果某种袜子现有x个，那么新加同一种袜子增加的方案数为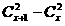。然后再展开:

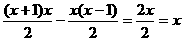
　　删除同理。

Code

 /**
  * bzoj
  * Problem2038
  * Accepted
  * Time:820ms
  * Memory:3264k
  */
 #include<iostream>
 #include<fstream>
 #include<sstream>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<ctime>
 #include<cctype>
 #include<cmath>
 #include<algorithm>
 #include<stack>
 #include<queue>
 #include<set>
 #include<map>
 #include<vector>
 using namespace std;
 typedef bool boolean;
 #define smin(a, b)    (a) = min((a), (b))
 #define smax(a, b)    (a) = max((a), (b))
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-' && x != -);
     if(x == -)    return;
     if(x == '-'){
         x = getchar();
         aFlag = -;
     }
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 typedef class Segment{
     public:
         int from;
         int end;
         int id;
         int index;
         Segment():from(), end(), index(){        }
         boolean operator < (Segment another) const{
             if(this->id != another.id)    return this->id < another.id;
             return this->end < another.end;
         }
 }Segment;

 int n, m;
 Segment* seg;
 int *colors;
 int divs;
 int blocks;

 inline long long C(int x){
     return (x * 1LL * (x - ) / );
 }

 template<typename T>
 inline T gcd(T a, T b){
     if(b == )    return a;
     return gcd(b, a % b);
 }

 inline void init(){
     readInteger(n);
     readInteger(m);
     seg = new Segment[(const int)(m + )];
     colors = new int[(const int)(n + )];
     divs = (int)(sqrt(n + 0.5));
     blocks = n / divs + (n % divs == ) ? () : ();
     for(int i = ; i <= n; i++){
         readInteger(colors[i]);
     }
     for(int i = ; i <= m; i++){
         readInteger(seg[i].from);
         readInteger(seg[i].end);
         seg[i].index = i;
         seg[i].id = seg[i].from / divs;
     }
 }

 int* ccolor;
 long long *resa, *resb;

 inline void solve(){
     sort(seg + , seg + m + );
     ccolor = new int[(const int)(n + )];
     resa = new long long[(const int)(m + )];
     resb = new long long[(const int)(m + )];
     int pseg = ;

     int mdzzf = , mdzzr = ;    //莫队指针，左闭右开
     long long qk = ;
     memset(ccolor, , sizeof(int) * (n + ));
     for(int i = ; i <= m; i++){
         if(seg[i].from == seg[i].end){
             resa[seg[i].index] = ;
             continue;
         }
         while(mdzzr > seg[pseg].end + )    qk -= --ccolor[colors[--mdzzr]];
         while(mdzzf > seg[pseg].from)    qk += ccolor[colors[--mdzzf]]++;
         while(mdzzr <= seg[pseg].end)    qk += ccolor[colors[mdzzr++]]++;
         while(mdzzf < seg[pseg].from)    qk -= --ccolor[colors[mdzzf++]];
         resa[seg[pseg].index] = qk;
         resb[seg[pseg].index] = C(seg[pseg].end - seg[pseg].from + );
         pseg++;
     }
     for(int i = ; i <= m; i++){
         if(resa[i] == ){
             printf("0/1\n");
             continue;
         }
         long long g = gcd(resa[i], resb[i]);
         printf("%lld/%lld\n", resa[i] / g, resb[i] / g);
     }
 }

 int main(){
     init();
     solve();
     return ;
 }