数字组合 · Combination Sum

不能重复：

［抄题］：

给出一个候选数字的set(C)和目标数字(T),找到C中所有的组合，使找出的数字和为T。C中的数字可以无限制重复被选取。

例如,给出候选数组[2,3,6,7]和目标数字7，所求的解为：

[7]，

[2,2,3]

［思维问题］：

1. 以为要在dfs函数中不断添加，其实用的是two sum的思想：反向寻找sum - nums[i]
2. 为了避免重复取数，需要先排序去重

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

［一刷］：

1. index和前面数不同时才+1，因此新数组容量需要+1
2. 如果remainTarget比nums[i]小，直接break，退出所有循环

［二刷］：

1. 数组要先排序，再去重
2. DFS中应该先是返回条件，再是循环中的循环退出条件。循环中的参数是i，不是startIndex，startIndex是所有数组的开头
3. combinations.add(nums[i]);添加的是数组中的元素，不是角标，毕竟是对元素进行处理

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

helper函数反复选i

［复杂度］：Time complexity: O() Space complexity: O()

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

public class Solution {
    /**
     * @param candidates: A list of integers
     * @param target:An integer
     * @return: A list of lists of integers
     */
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> results = new ArrayList<>();
        if (candidates == null || candidates.length == 0) {
            return results;
        }

        int[] nums = removeDuplicates(candidates);

        dfs(nums, 0, new ArrayList<Integer>(), target, results);

        return results;
    }

    private int[] removeDuplicates(int[] candidates) {
        Arrays.sort(candidates);

        int index = 0;
        for (int i = 0; i < candidates.length; i++) {
            if (candidates[i] != candidates[index]) {
                candidates[++index] = candidates[i];
            }
        }

        int[] nums = new int[index + 1];
        for (int i = 0; i < index + 1; i++) {
            nums[i] = candidates[i];
        }

        return nums;
    }

    private void dfs(int[] nums,
                     int startIndex,
                     List<Integer> combination,
                     int remainTarget,
                     List<List<Integer>> results) {
        if (remainTarget == 0) {
            results.add(new ArrayList<Integer>(combination));
            return;
        }

        for (int i = startIndex; i < nums.length; i++) {
            if (remainTarget < nums[i]) {
                break;
            }
            combination.add(nums[i]);
            dfs(nums, i, combination, remainTarget - nums[i], results);
            combination.remove(combination.size() - 1);
        }
    }
}

能重复：

［抄题］：

［思维问题］：

知道：不用remove duplicate函数。先排序，helper函数中改成i+1

结果：

[7,1,2,5,1,6,10]
8

输出[[1,1,6],[1,2,5],[1,7],[1,2,5],[1,7],[2,6]]

期望[[1,1,6],[1,2,5],[1,7],[2,6]]

问题：不知道怎么结果去重

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

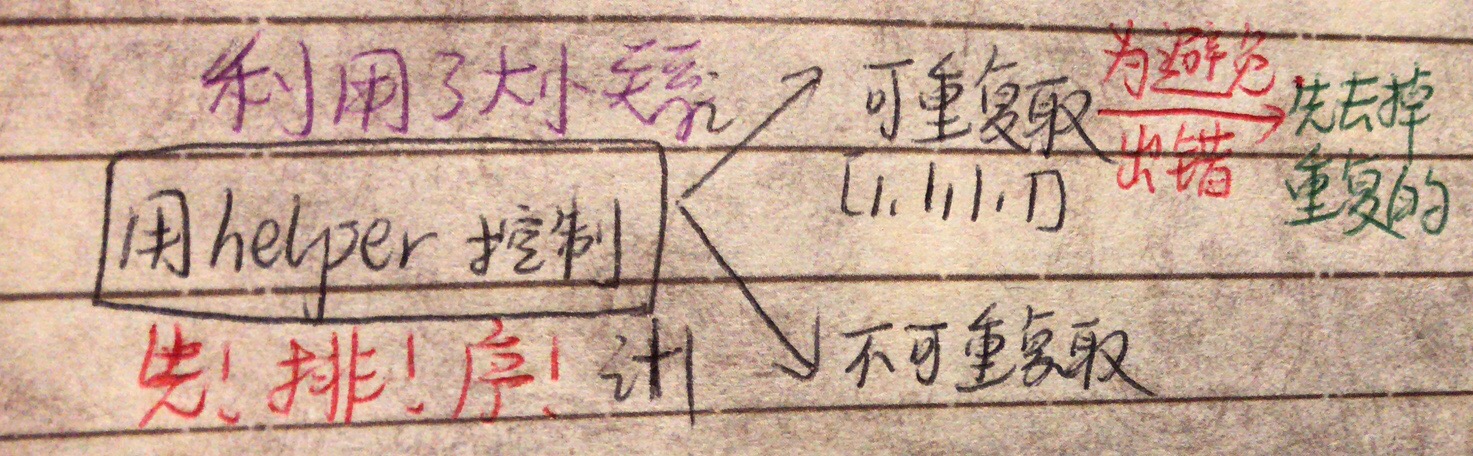
［一刷］：

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

［复杂度］：Time complexity: O() Space complexity: O()

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

public class Solution {
    /**
     * @param num: Given the candidate numbers
     * @param target: Given the target number
     * @return: All the combinations that sum to target
     */
    public List<List<Integer>> combinationSum2(int[] candidates,
            int target) {
        List<List<Integer>> results = new ArrayList<>();
        if (candidates == null || candidates.length == 0) {
            return results;
        }

        Arrays.sort(candidates);
        List<Integer> combination = new ArrayList<Integer>();
        helper(candidates, 0, combination, target, results);

        return results;
    }

    private void helper(int[] candidates,
                        int startIndex,
                        List<Integer> combination,
                        int target,
                        List<List<Integer>> results) {
        if (target == 0) {
            results.add(new ArrayList<Integer>(combination));
            return;
        }

        for (int i = startIndex; i < candidates.length; i++) {
            if (i != startIndex && candidates[i] == candidates[i - 1]) {
                continue;
            }
            if (target < candidates[i]) {
                break;
            }
            combination.add(candidates[i]);
            helper(candidates, i + 1, combination, target - candidates[i], results);
            combination.remove(combination.size() - 1);
        }
    }
}