洛谷P2569 股票交易【dp】【单调队列】

题目描述

最近 \text{lxhgww}lxhgww 又迷上了投资股票，通过一段时间的观察和学习，他总结出了股票行情的一些规律。

通过一段时间的观察，\text{lxhgww}lxhgww 预测到了未来 TT 天内某只股票的走势，第 ii 天的股票买入价为每股 AP_iAPi，第 ii 天的股票卖出价为每股 BP_iBPi（数据保证对于每个 ii，都有 AP_i \geq BP_iAPi≥BPi），但是每天不能无限制地交易，于是股票交易所规定第 ii 天的一次买入至多只能购买 AS_iASi 股，一次卖出至多只能卖出 BS_iBSi 股。

另外，股票交易所还制定了两个规定。为了避免大家疯狂交易，股票交易所规定在两次交易（某一天的买入或者卖出均算是一次交易）之间，至少要间隔 WW 天，也就是说如果在第 ii 天发生了交易，那么从第 i+1i+1 天到第 i+Wi+W 天，均不能发生交易。同时，为了避免垄断，股票交易所还规定在任何时间，一个人的手里的股票数不能超过 \text{MaxP}MaxP。

在第 11 天之前，\text{lxhgww}lxhgww 手里有一大笔钱（可以认为钱的数目无限），但是没有任何股票，当然，TT 天以后，\text{lxhgww}lxhgww 想要赚到最多的钱，聪明的程序员们，你们能帮助他吗？

输入输出格式

输入格式：

输入数据第一行包括 33 个整数，分别是 TT，\text{MaxP}MaxP，WW。

接下来 TT 行，第 ii 行代表第 i-1i−1 天的股票走势，每行 44 个整数，分别表示 AP_i,\ BP_i,\ AS_i,\ BS_iAPi, BPi, ASi, BSi。

输出格式：

输出数据为一行，包括 11 个数字，表示 \text{lxhgww}lxhgww 能赚到的最多的钱数。

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

对于 30\%30% 的数据，0\leq W<T\leq 50,1\leq\text{MaxP}\leq500≤W<T≤50,1≤MaxP≤50

对于 50\%50% 的数据，0\leq W<T\leq 2000,1\leq\text{MaxP}\leq500≤W<T≤2000,1≤MaxP≤50

对于 100\%100% 的数据，0\leq W<T\leq 2000,1\leq\text{MaxP}\leq20000≤W<T≤2000,1≤MaxP≤2000

对于所有的数据，1\leq BP_i\leq AP_i\leq 1000,1\leq AS_i,BS_i\leq\text{MaxP}1≤BPi≤APi≤1000,1≤ASi,BSi≤MaxP

题意：

一共t天，最多可以持有maxp支股票。给定每天股票买入卖出价格和每天的交易限额。问可以最多赚多少钱。

思路：

应该能够想得到这是一个dp。子结构就是前i天能赚取的最多价格，这就是“阶段”，也就是第一维。同时我们还需要记录一下持有的股票数，因为状态转移时，不同的股票数的转移是不同的。

因此，dp[i][j]表示第i天持有j的时候所能赚取的最大值。

对于每一天我们都有三种情况。

1.不买也不卖。那么转移方程就是

2.买入。买入有分两种情况，一种是之前什么都没有，这j股都是在第i天买的。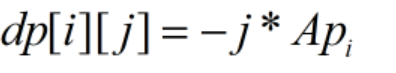

　　另一种是之前的某一天买了k股，今天买了j-k股。而且题目要求两个交易的日子要间隔w天。

3.卖出。之前的某一天有k股，卖掉了k-j股，第i天剩下j股。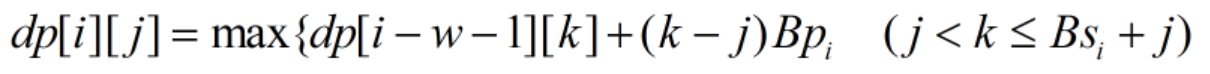

但是我们会发现状态转移的时候如果枚举k，会出现O(n^3)的复杂度，需要进一步优化。

观察状态转移方程我们可以把k合并同类项，比如卖出的式子可以变成

由于max{}中的是一个正数，假设我们设在j时这个值为x，扩展到j+1时，我们只有可能取x或者k=j时的值。他是一个递增的选择。

就可以用单调队列来维护这个值了。

由于卖出是由比j大的k推出的，所以在转移卖出这种情况的时候，j应该是逆序的。

 #include <iostream>

 #include <set>

 #include <cmath>

 #include <stdio.h>

 #include <cstring>

 #include <algorithm>

 #include <vector>

 #include <queue>

 #include <map>

 #include <bits/stdc++.h>

 using namespace std;

 typedef long long LL;

 #define inf 0x7f7f7f7f

 const int maxn = ;

 int t, maxp, w;

 struct node{

     int ap, bp, as, bs;

 }day[maxn];

 int dp[maxn][maxn], que[maxn];

 int main()

 {

     scanf("%d%d%d", &t, &maxp, &w);

     memset(dp, -inf, sizeof(dp));

     for(int i = ; i <= t; i++){

         scanf("%d%d%d%d", &day[i].ap, &day[i].bp, &day[i].as, &day[i].bs);

     }

     for(int i = ; i <= t; i++){

         for(int j = ; j <= day[i].as; j++){

             dp[i][j] = -j * day[i].ap;

         }

         for(int j = ; j <= maxp; j++){

             dp[i][j] = max(dp[i][j], dp[i - ][j]);

         }

         if(i <= w)continue;

         int head = , tail = ;

         for(int j = ; j <= maxp; j++){

             while(dp[i - w - ][que[tail]] + que[tail] * day[i].ap <= dp[i -  - w][j] + j * day[i].ap && head <= tail){

                 tail--;

             }

             que[++tail] = j;

             while(j - que[head] > day[i].as){

                 head++;

             }

             dp[i][j] = max(dp[i][j], dp[i - w - ][que[head]] - (j - que[head]) * day[i].ap);

         }

         head = , tail = ;

         for(int j = maxp; j >= ; j--){

             while(dp[i - w - ][que[tail]] + que[tail] * day[i].bp <= dp[i -  - w][j] + j * day[i].bp && head <= tail){

                 tail--;

             }

             que[++tail] = j;

             while(que[head] - j > day[i].bs){

                 head++;

             }

             dp[i][j] = max(dp[i][j], dp[i -  - w][que[head]] + (que[head] - j) * day[i].bp);

         }

     }

     int ans = -;

     for(int j = ; j <= maxp; j++){

         ans = max(ans, dp[t][j]);

     }

     printf("%d\n", ans);

     return ;

 }