[Leetcode] Unique binary search trees 唯一二叉搜索树

Given n, how many structurally unique BST's (binary search trees) that store values 1...n?

For example,
Given n = 3, there are a total of 5 unique BST's.

  1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

题意：给定数n，二叉树的结点的值分别为1,2....n。问能组成多少种不同的二叉搜索树。

二叉搜索树的性质为：在任一结点r的左（右）子树中，所有结点（若存在）均小于（大于）r。更一般性的特点是：任何一棵二叉树是二叉搜索树，当且仅当其中序遍历序列单调非降。

恩，一看，一想不会，好吧，又要找大神们了。

方法一：递归

思路：空树和只有根节点时，也为BST。对于一点i，当其为根节点时，左子树的节点的个数为i-1，（为1,...i-1）,右子树的个数为n-i（为，i+1,...n）。对一个根来说，唯一二叉树的个数为左子树结点的个数乘以右子树的个数。而根节点可以从1到n 中选择。

 class Solution {
 public:
     int numTrees(int n)
     {
         if(n<=)    return ;
         int sum=;
         for(int i=;i<=n;++i)
             sum+=numTrees(i-)*numTrees(n-i);

         return sum;
     }
 };

方法二：

还有大神说这是Catalan Number卡特兰数的一个例子。卡特兰数的的递推公式：

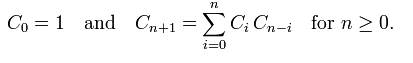
可以使用动态规划解决问题。维护向量sumNode，sumNode(i)为结点个数为i时，唯一二叉搜索树的个数。和这题相对应的意义，可以写出n较小的情况。

 class Solution {
 public:
     int numTrees(int n)
     {
         vector<int> sumNode(n+,);
         sumNode[]=;
         sumNode[]=;

         for(int i=;i<=n;++i)
             for(int j=;j<i;++j)　　//j符合条件时，最大为i-1，对照公式
                 sumNode[i]+=sumNode[j]*sumNode[i-j-];

         return sumNode[n];
     }
 };