Weibull分布(韦伯分布、威布尔分布)

log函数

从概率论和统计学角度看，Weibull Distribution是连续性的概率分布，其概率密度为：

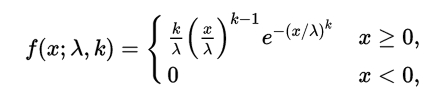
其中，x是随机变量，λ＞0是比例参数（scale parameter），k＞0是形状参数（shape parameter）。显然，它的累积分布函数是扩展的指数分布函数，而且，Weibull distribution与很多分布都有关系。如，当k=1，它是指数分布；k=2时，是Rayleigh distribution(瑞利分布)。

Weibull概率密度函数

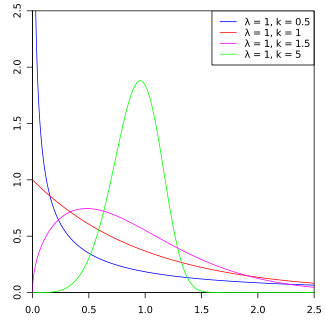
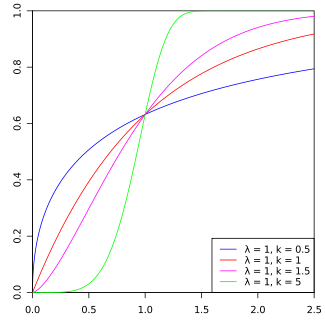
k <1的值表示故障率随时间减小。如果存在显着的“婴儿死亡率”或有缺陷的物品早期失效，并且随着缺陷物品被除去群体，故障率随时间降低，则发生这种情况。在创新扩散的背景下，这意味着负面的口碑：危险功能是采用者比例的单调递减函数;
k = 1的值表示故障率随时间是恒定的。这可能表明随机外部事件正在导致死亡或失败。威布尔分布减小到指数分布;
k> 1的值表示故障率随时间增加。如果存在“老化”过程，或者随着时间的推移更可能失败的部分，就会发生这种情况。在创新扩散的背景下，这意味着积极的口碑：危险功能是采用者比例的单调递增函数。该函数首先是凹的，然后是凸的，拐点为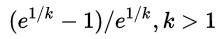

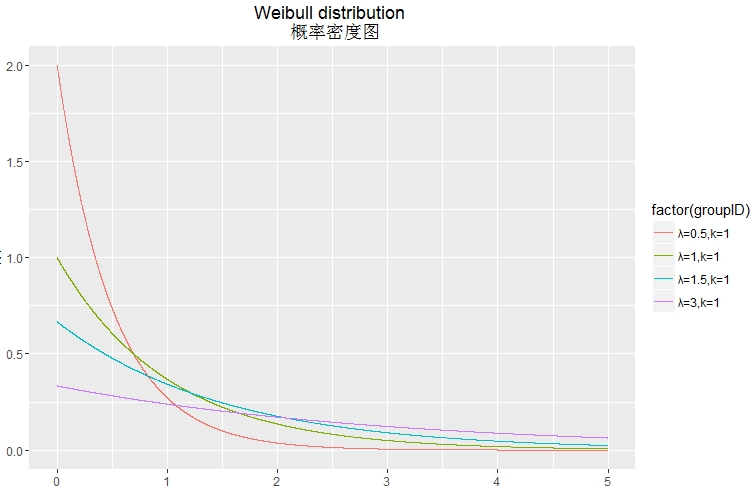
Weibull累计分布函数