牛客网暑期ACM多校训练营（第七场）J题(Sudoku Subrectangles)题解

一、题意

给定一个高度为$n$，宽度为$m$的字母矩形(有大写和小写字母，共$52$种)，问里面有多少个子矩形是“数独矩形”。数独矩形是指，该矩形内每一行内元素都不相同，每一列内元素也不相同。

二、思路

对于每一个点$(i, j)$，预处理出$R[i][j]$，表示在第$i$行从第$j$列开始，往右一直到$R[i][j]$位置，这一段内所有元素都不相同。同理，再预处理出$D[i][j]$，表示在第$j$列从第$i$行开始，往下一直到$D[i][j]$位置，这一段内所有元素都不相同。显然，无论是往右还是往下这样的一段，长度都不会超过$52$。形式表示就是，$max\{R[i][j]\}=52(1 \le i \le n,1 \le j \le m)$，$max\{D[i][j]\}=52(1 \le i \le n,1 \le j \le m)$。

所以这部分的ACM版时间复杂度为$O(52*n*m)$。

接下来，枚举每一个点$(i, j)$，统计以点$(i, j)$作为左上角的数独矩形的个数。记住，一定要以点$(i, j)$作为左上角。

示意图如下，其中，绿色竖条代表$D[i][k](j \le k \le R[i][j])$，黄色横点条代表$R[k][j](i \le k \le D[i][j])$。

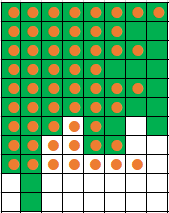
从$i$开始枚举每一行(显然只需要枚举到$D[i][j]$即可，最多循环$52$次)，从第$i$行开始，记录一个右边界minr，表示：所有以$(i, j)$为左上角的行数为$k-i+1$的数独矩形最右边可到达的边界。假设当前在第$k$行，当前的右边界为$minr$，那么，所有以$(i, j)$为左上角的行数为$k-i+1$的数独矩形的个数为$minr-j+1$。举个例子，对于上图中，假设左上角坐标为$(i, j)$，当前枚举的行号$k=i$，则$minr=j+7$，这一行中数独矩形的个数为$minr-j+1=8$个，也就是$[(i, j)], [(i, j), (i, j+1)], [(i, j), (i, j+1), (i, j+2)], \dots, [(i, j), (i, j+1), (i, j+2), \dots, (i, minr)]$。

当枚举的行号$k=i+1$时，此时$minr=j+5=R[k][j]$，行数为两行(第$i$行和第$i+1$行)中数独矩形的个数为$minr-j+1=6$个。也就是：

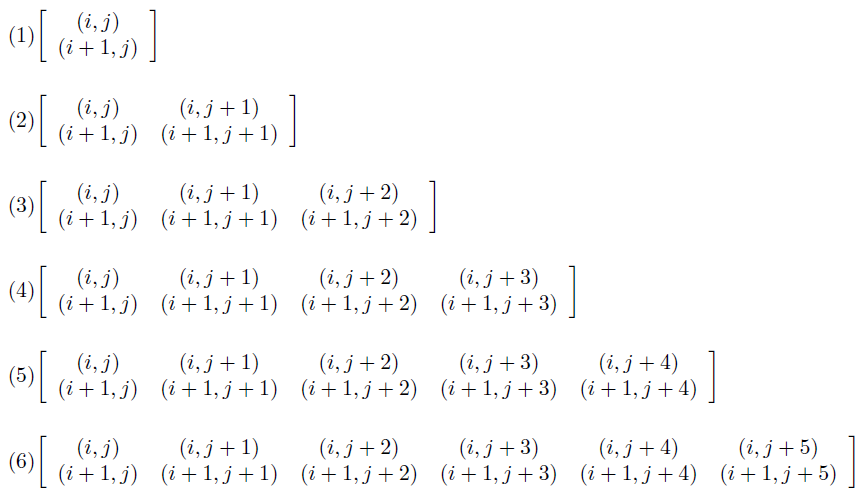
后面的同理。然后，要注意的是，当$min\{D[i][k]\}(j \le k \le minr) < k$($j$~$minr$之间的最短的绿色竖条到不了$k$)或者$R[k][j] < minr$(第$k$行的黄色横点条到不了$minr$)时，说明以点$(i, j)$为左上角的高度为$k-i+1$的数独矩形的个数没有$minr-j+1$个，需要减小$minr$。

总的ACM版时间复杂度为$O(52*n*m)$。

三、代码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 1010
char s[MAXN][MAXN];
int n, m, R[MAXN][MAXN], D[MAXN][MAXN];
int main() {
//    freopen("input.txt", "r", stdin);
//    freopen("output2.txt", "w", stdout);
    scanf("%d%d", &n, &m);
    ; i <= n; ++i) {
        scanf();
        ; j <= m; ++j) {
            ;
            ;
        }
    }
    ; i <= n; ++i) {
        ; j <= m; ++j) {
            , m), k = j;
            ;
            for(k = j; k <= r; ++k) {
                ))b |= 1LL << s[i][k];
                else {
                    R[i][j] = k - ;
                    break;
                }
            } )R[i][j] = k - ;
        }
    }
    ; j <= m; ++j) {
        ; i <= n; ++i) {
            , n), k = i;
            ;
            for(k = i; k <= r; ++k) {
                ))b |= 1LL << s[k][j];
                else {
                    D[i][j] = k - ;
                    break;
                }
            } )D[i][j] = k - ;
        }
    }
    ;
    ];
    ; i <= n; ++i) {
        ; j <= m; ++j) {
            , min(R[i][j], m)), k = j, minr;
            mind[] = D[i][j];
            ; k <= r; ++k) {
                mind[k - j] = min(mind[k - j - ], D[i][k]);
            }
            r = min(i + , min(D[i][j], n)), k = i, minr = R[i][j];
            for(k = i; k <= r; ++k) {
                while(minr > j && (R[k][j] < minr || mind[minr - j] < k))minr--;
                ans += minr - j + ;
            }
        }
    }
    cout << ans << '\n';
    ;
}