MATLAB拟合和插值

定义

插值和拟合：

曲线拟合是指您拥有散点数据集并找到最适合数据一般形状的线（或曲线）。

插值是指您有两个数据点并想知道两者之间的值是什么。中间的一半是他们的平均值，但如果你只想知道两者之间的四分之一，你必须插值。

拟合

我们着手写一个线性方程图的拟合：

y=3x^3+2x^2+x+2

首先我们生成一组数据来分析：

x=-5:0.5:5;
e=50*rand(1,length(x))-25;%制造[-25,25]的随机数作为误差
y=3*x.^3+2*x.^2+x+2+e;%得到y值
plot(x,y,'.')

x =

  Columns 1 through 6

   -5.0000   -4.5000   -4.0000   -3.5000   -3.0000   -2.5000

  Columns 7 through 12

   -2.0000   -1.5000   -1.0000   -0.5000         0    0.5000

  Columns 13 through 18

    1.0000    1.5000    2.0000    2.5000    3.0000    3.5000

  Columns 19 through 21

    4.0000    4.5000    5.0000

y =

  Columns 1 through 6

 -350.0110 -248.6360 -169.3421  -89.5653  -88.2298  -57.7238

  Columns 7 through 12

  -32.5505    2.3308   11.5861    9.0123   -0.4538    5.7254

  Columns 13 through 18

   -2.1840   30.3596   20.4478   73.2138   88.1756  152.0492

  Columns 19 through 21

  236.2809  334.3864  411.0563

这时候x,y作为已知数据存在，要求我们拟合x,y的散点图，这时候会用到polyfit这个函数。

语法

p = polyfit(x,y,n)
[p,S] = polyfit(x,y,n)
[p,S,mu] = polyfit(x,y,n)

说明

p = polyfit(x,y,n) 返回阶数为 n 的多项式 p(x) 的系数，该阶数是 y 中数据的最佳拟合（在最小二乘方式中）。p 中的系数按降幂排列，p 的长度为 n+1

[p,S] = polyfit(x,y,n) 还返回一个结构体 S，后者可用作 polyval 的输入来获取误差估计值。

[p,S,mu] = polyfit(x,y,n) 还返回 mu，后者是一个二元素向量，包含中心化值和缩放值。mu(1) 是 mean(x)，mu(2) 是 std(x)。使用这些值时，polyfit 将 x 的中心置于零值处并缩放为具有单位标准差

plot(x,y,'.')%已知数据的散点图
hold on
d=polyfit(x,y,2);%进行线性拟合，假设函数为二次函数
y1=d(1)*x.^2+d(2)*x+d(3);
plot(x,y1)//绘制猜测的函数

　　

明显不符合，我们继续猜测

plot(x,y,'.')
hold on
d=polyfit(x,y,3);
y1=d(1)*x.^3+d(2)*x.^2+d(3)*x+d(4);
plot(x,y1)

拟合成功。

插值

一维插值

以上面的数据为例子

x=-5:0.5:5;
e=50*rand(1,length(x))-25;%制造[-25,25]的随机数作为误差
y=3*x.^3+2*x.^2+x+2+e;%得到y值
%插值
x2=-5:0.1:5;
y2=interp1(x,y,'x2,'spline');
plot(x2,y2,'r+')

二维插值

语法

[X,Y] = meshgrid(x,y)

[X,Y] = meshgrid(x)

[X,Y,Z] = meshgrid(x,y,z)

[X,Y,Z] = meshgrid(x)

说明

[X,Y] = meshgrid(x,y) 基于向量 x 和 y 中包含的坐标返回二维网格坐标。X 是一个矩阵，每一行是 x 的一个副本；Y 也是一个矩阵，每一列是 y 的一个副本。坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。

[X,Y] = meshgrid(x) 与 [X,Y] = meshgrid(x,x) 相同，并返回网格大小为 length(x)×length(x) 的方形网格坐标。

[X,Y,Z] = meshgrid(x,y,z) 返回由向量 x、y 和 z 定义的三维网格坐标。X、Y 和 Z 表示的网格的大小为 length(y)×length(x)×length(z)。

[X,Y,Z] = meshgrid(x) 与 [X,Y,Z] = meshgrid(x,x,x) 相同，并返回网格大小为 length(x)×length(x)×length(x) 的三维网格坐标。

我们先绘制一个三维的图像

[x,y]=meshgrid(-5:1:5,-10:2:10);
z=12-x.^3-y.^3;
surf(x,y,z)

给人的感觉是很“粗糙”的，这时候我们使用插值，增加数据。

[x0,y0]=meshgrid(-5:0.2:5,-10:0.4:10);
z0=interp2(x,y,z,x0,y0,'spline');
surf(x0,y0,z0)

例题

例1

1、已知以下实验测量数据，

\* MERGEFORMAT	1	1.5	2.5	3	4.5
\* MERGEFORMAT	-0.86	13.66	90.25	152.57	473.70

（1）请画出以上数据的散点图；

（2）请用合适的多项式拟合上述数据；

（3）请用三次样条一次插值以上数据.

2、已知网格化数据如下：

\* MERGEFORMAT \* MERGEFORMAT	-1	-0.5	0	0.5	1
-2	1.77	1.12	0.32	0.44	-2.35
-1	1.62	1.29	0.94	-1.49	-0.78
0	0.23	-1.01	-0.74	1.08	-0.13
1	-0.61	-0.41	-0.63	-0.05	1.44
2	-2.94	-0.22	0.56	0.17	1.73

请用三次样条二次插值法插出更光滑精细的曲面.

答案

%1-(1)
clc,clear
x=[1 1.5	2.5 3 4.5];
y=[-0.86	13.66 90.25 152.57 473.70];
plot(x,y,'.');

%1-(2)
d=polyfit(x,y,1);
y1=d(1)*x+d(2);
plot(x,y,'.');
plot(x,y1);%对比线性图与散点图，发现不匹配
d=polyfit(x,y,2);
y1=d(2)*x.^2+d(2)*x+d(3);
plot(x,y,'.');
plot(x,y1);%对比线性图与散点图，发现匹配成功，拟合完成

%1-(3)
x=[1 1.5 2.5 3 4.5];
y=[-0.86	13.66 90.25 152.57 473.70];
x1=[1:0.1:4.5];
y1=interp1(x,y,x1,'spline');
plot(x,y,x1,y1);

%2
[x1,y1]=meshgrid(-2:1:2,-1:0.5:1);
z1=[1.77 1.21 0.32 0.44 -2.35;1.62 1.29 0.94 -1.49 -0.78;0.23 -1.01 -0.74 1.08 -0.13;...
-0.61 -0.41 -0.63 -0.05 1.44;-2.94 -0.22 0.56 0.17 1.73];
surf(x1,y1,z1)
[x,y]=meshgrid(-1:0.1:1, -2:0.2:2);
z=interp2(x1,y1,z1,x,y,'spline');
surf(x,y,z)

例2

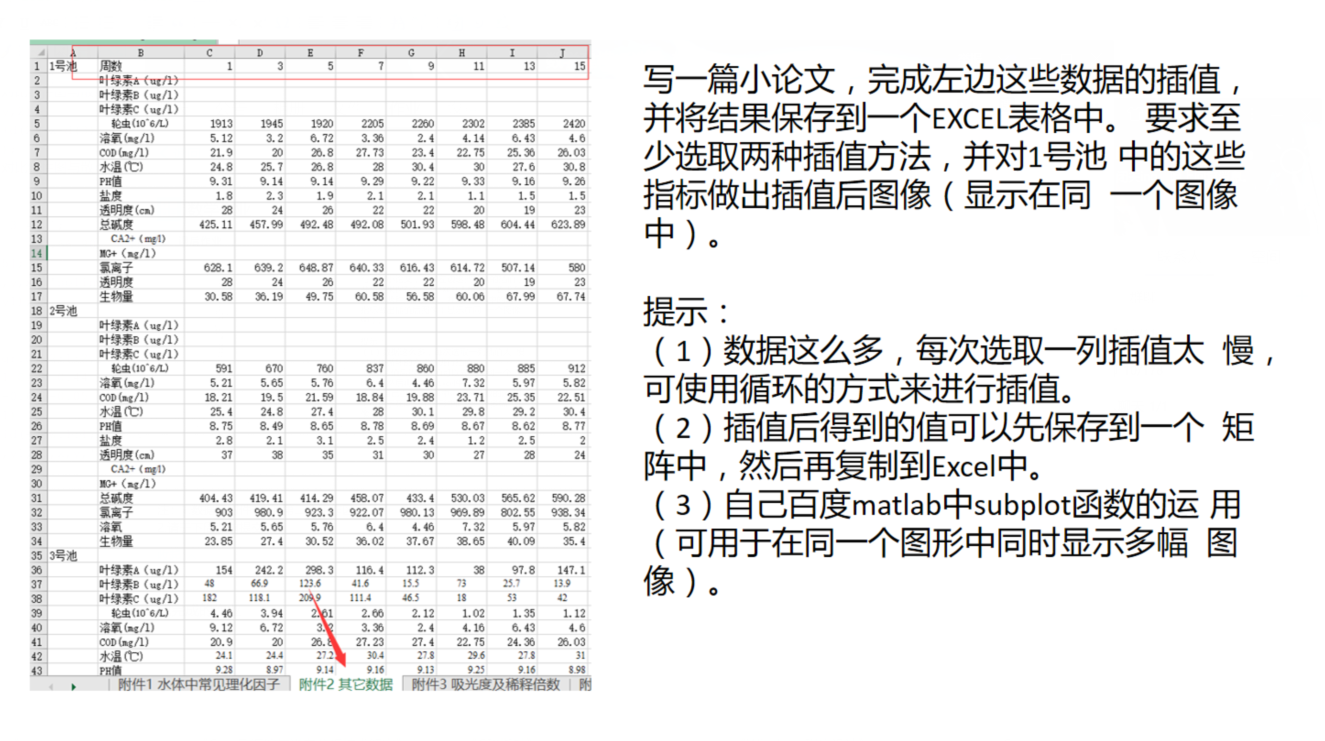
数据：点击下载

实际任务就是sheet2中中的元素，只给了单周的元素数据，没有给偶数周，这就需要我们插值出来

答案

clc,clear
%% 读取数据
ydatas = xlsread('data1.xls',2,'C5:J17');
% 清除无效数据
ydatas(9:10,:)=[];

%% 绘图准备
% y坐标轴名称
yname = ["周数","轮虫(10^6/L)","溶氧(mg/l)","COD(mg/l)","水温(℃)","PH值","盐度","透明度(cm)","总碱度","氯离子","透明度","生物量"];
% yname = {'轮虫(10^6/L)','溶氧(mg/l)','COD(mg/l)','水温(℃)','PH值','盐度','透明度(cm)','总碱度','氯离子','透明度','生物量'};
% x坐标
xdatas =  1:2:15;
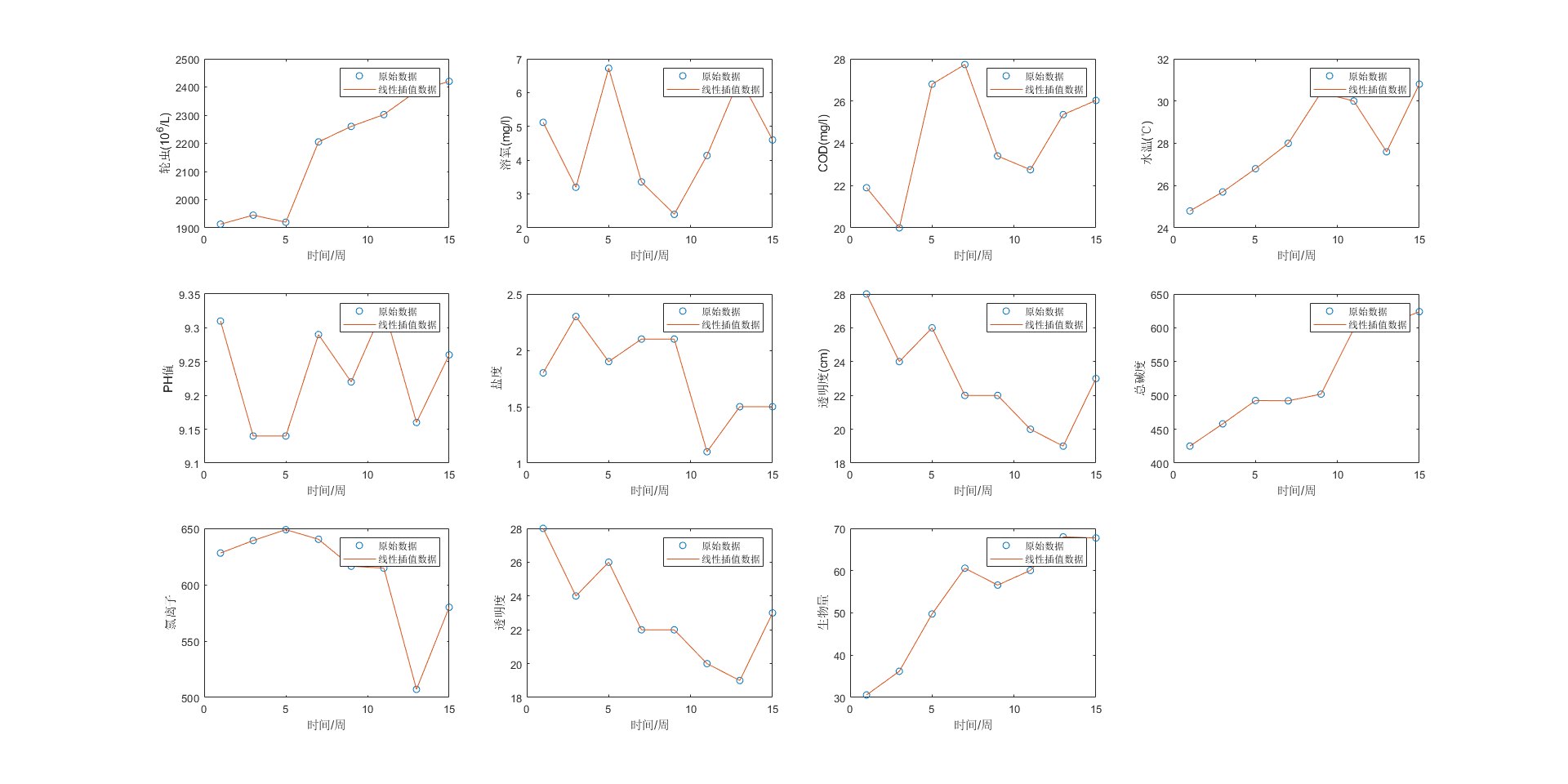
xval = 1:15;

%% 线性插值
figure(1)
yval1 = [];
for index=1:11
    tmp = interp1(xdatas,ydatas(index,:),xval,'linear');
    yval1 = [yval1;tmp];
    subplot(3,4,index)
    plot(xdatas,ydatas(index,:),'*',xval,tmp,'--r')
    xlabel('时间/周');
    ylabel(yname(index+1))
    legend('原始数据','线性插值数据')
end

%% 三次样条插值
figure(2)
yval2 = [];
for index=1:11
    tmp = interp1(xdatas,ydatas(index,:),xval,'spline');
    yval2 = [yval2;tmp];
    subplot(3,4,index)
    plot(xdatas,ydatas(index,:),'*',xval,tmp,'--r')
    xlabel('时间/周');
    ylabel(yname(index+1))
    legend('原始数据','三次样条插值数据')
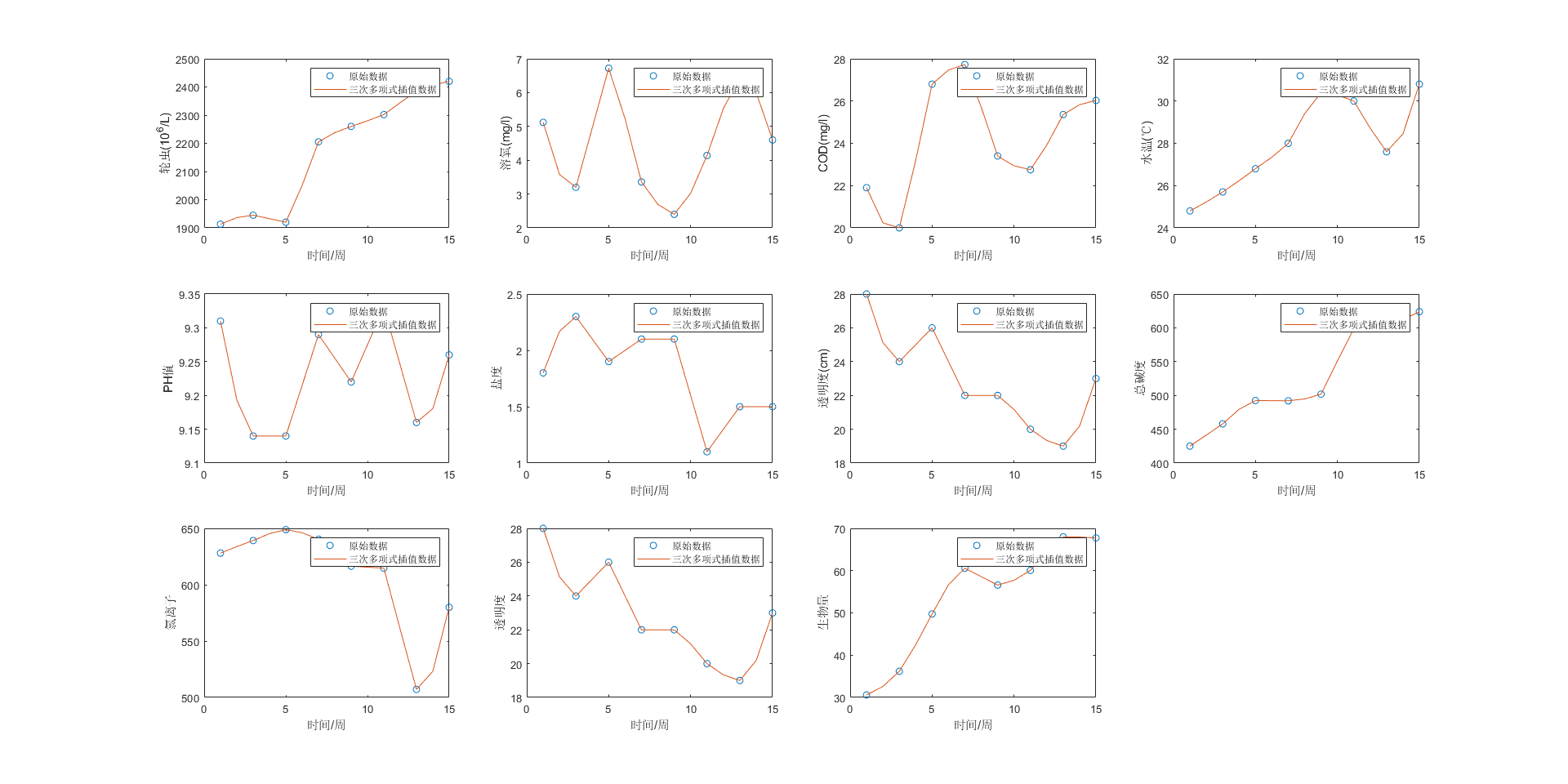
end

%% 三次多项式插值
figure(3)
yval3 = [];
for index=1:11
    tmp = interp1(xdatas,ydatas(index,:),xval,'pchip');
    yval3 = [yval3;tmp];
    subplot(3,4,index)
    plot(xdatas,ydatas(index,:),'*',xval,tmp,'--r')
    xlabel('时间/周');
    ylabel(yname(index+1))
    legend('原始数据','三次多项式插值数据')
end
%% 数据存储
new_data1 = [xval;yval1];
new_data1 = [yname',new_data1];
xlswrite('output.xls',new_data1,'Sheet1');
new_data2 = [xval;yval2];
new_data2 = [yname',new_data2];
xlswrite('output.xls',new_data2,'Sheet2');
new_data3 = [xval;yval3];
new_data3 = [yname',new_data3];
xlswrite('output.xls',new_data3,'Sheet3');

输出结果数据：https://www.lanzous.com/iau54la

例3

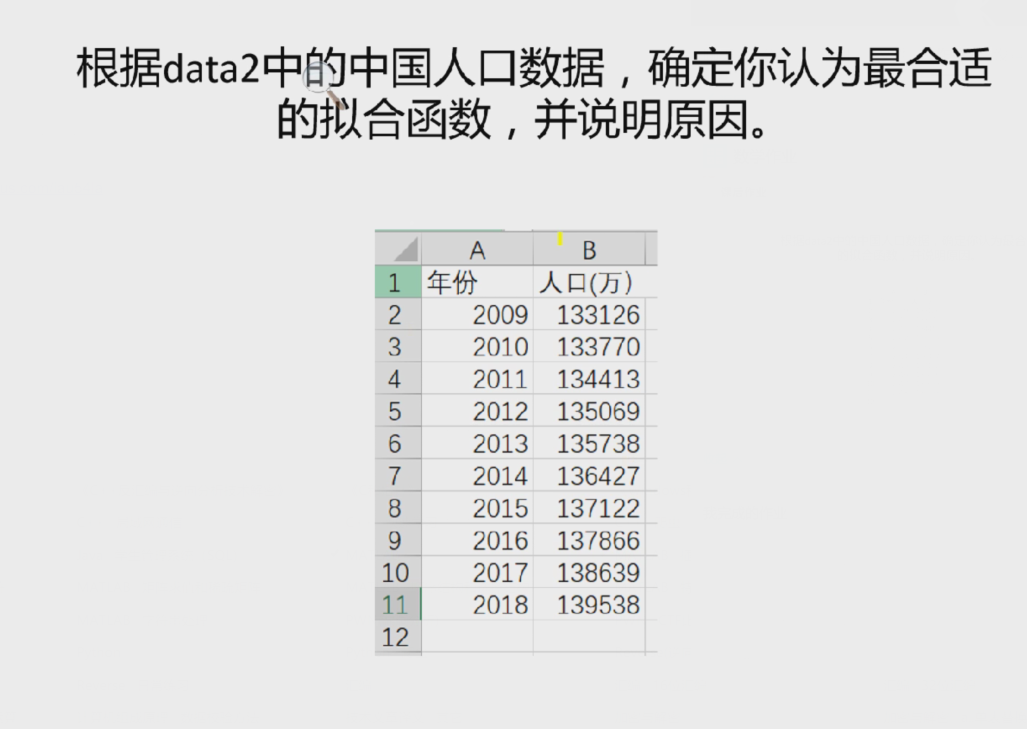
数据下载：点击下载

答案

clc,clear
%%
xdatas = xlsread('data2.xlsx','A2:A11');
ydatas = xlsread('data2.xlsx','B2:B11');
a=polyfit(xdatas,ydatas,1);
y1=a(1)*xdatas+a(2);
subplot(3,2,1)
plot(xdatas,y1,'r-',xdatas,ydatas,'*')
title('一次拟合');
xlabel('年份');
ylabel('人口/万');
y1_datas = a(1)*xdatas+a(2);
ssr1 = sum((y1_datas-mean(ydatas)).^2);
sst1 = sum((ydatas-mean(ydatas)).^2);
r1_sq = ssr1/sst1;
txt = ['R^2=' num2str(r1_sq)];
text(2010,138000,txt)

%%
b=polyfit(xdatas,ydatas,2);
y2=b(1)*xdatas.^2+b(2)*xdatas+b(3);
subplot(3,2,2)
plot(xdatas,y2,'r-',xdatas,ydatas,'*')
title('二次拟合');
xlabel('年份');
ylabel('人口/万');
y2_datas = b(1)*xdatas.^2+b(2)*xdatas+b(3);
ssr2 = sum((y2_datas-mean(ydatas)).^2);
sst2 = sum((ydatas-mean(ydatas)).^2);
r2_sq = ssr2/sst2;
txt = ['R^2=' num2str(r2_sq)];
text(2010,138000,txt)

%%
c=polyfit(xdatas,ydatas,3);
y3=c(1)*xdatas.^3+c(2)*xdatas.^2+c(3)*xdatas+c(4);
subplot(3,2,3)
plot(xdatas,y3,'r-',xdatas,ydatas,'*')
title('三次拟合');
xlabel('年份');
ylabel('人口/万');
y3_datas = c(1)*xdatas.^3+c(2)*xdatas.^2+c(3)*xdatas+c(4);
ssr3 = sum((y3_datas-mean(ydatas)).^2);
sst3 = sum((ydatas-mean(ydatas)).^2);
r3_sq = ssr3/sst3;
txt = ['R^2=' num2str(r3_sq)];
text(2010,138000,txt)

%%
d=polyfit(xdatas,ydatas,4);
y4=d(1)*xdatas.^4+d(2)*xdatas.^3+d(3)*xdatas.^2+d(4)*xdatas+d(5);
subplot(3,2,4)
plot(xdatas,y4,'r-',xdatas,ydatas,'*')
title('四次拟合');
xlabel('年份');
ylabel('人口/万');
y4_datas = d(1)*xdatas.^4+d(2)*xdatas.^3+d(3)*xdatas.^2+d(4)*xdatas+d(5);
ssr4 = sum((y4_datas-mean(ydatas)).^2);
sst4 = sum((ydatas-mean(ydatas)).^2);
r4_sq = ssr4/sst4;
txt = ['R^2=' num2str(r4_sq)];
text(2010,138000,txt)

%%
e=polyfit(xdatas,ydatas,5);
y5=e(1)*xdatas.^5+e(2)*xdatas.^4+e(3)*xdatas.^3+e(4)*xdatas.^2+e(5)*xdatas+e(6);
subplot(3,2,5)
plot(xdatas,y5,'r-',xdatas,ydatas,'*')
title('五次拟合');
xlabel('年份');
ylabel('人口/万');
y5_datas = e(1)*xdatas.^5+e(2)*xdatas.^4+e(3)*xdatas.^3+e(4)*xdatas.^2+e(5)*xdatas+e(6);
ssr5 = sum((y5_datas-mean(ydatas)).^2);
sst5 = sum((ydatas-mean(ydatas)).^2);
r5_sq = ssr5/sst5;
txt = ['R^2：' num2str(r5_sq)];
text(2010,138000,txt)

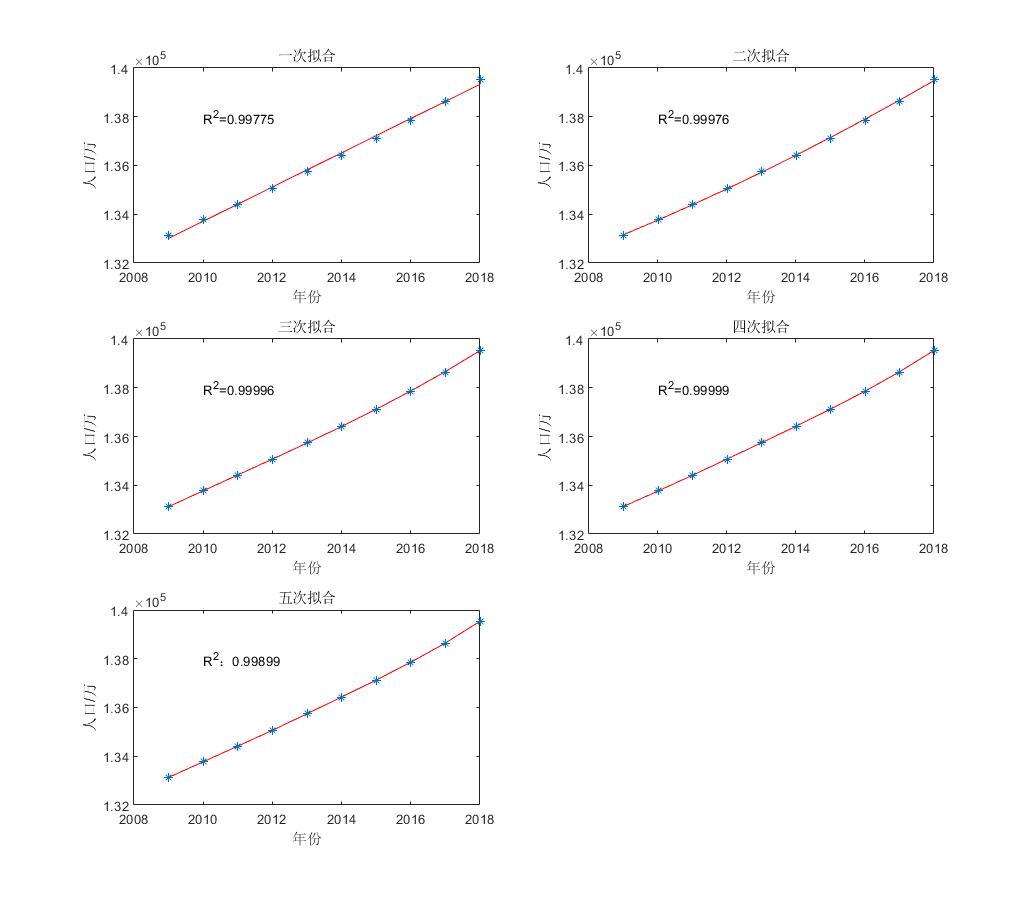
通过对数据拟合，对比确定系数，反应拟合效果，确定出最佳拟合函数为四次拟合函数：y = 0.26*x^4-2.06*x^3+6.21*x^2-8.32*x+4.19