ONTAK2010 Peaks加强版(离线&在线)

题面

弱化版:luogu

强制在线版:bzoj

题解

本题有两种解法

离线算法:线段树合并

先看一道简单题[USACO18JAN]MooTube

本题就是在此基础上求第\(k\)高的点

首先把询问和路径都排一下序

然后记一个指针,如果当前路径可以对这个询问有贡献,就加入这条边

本题也是一样

在此基础上,线段树合并即可求第\(k\)高的点

Code

#include<bits/stdc++.h>

#define LL long long
#define RG register

using namespace std;
template<class T> inline void read(T &x) {
	x = 0; RG char c = getchar(); bool f = 0;
	while (c != '-' && (c < '0' || c > '9')) c = getchar(); if (c == '-') c = getchar(), f = 1;
	while (c >= '0' && c <= '9') x = x*10+c-48, c = getchar();
	x = f ? -x : x;
	return ;
}
template<class T> inline void write(T x) {
	if (!x) {putchar(48);return ;}
	if (x < 0) x = -x, putchar('-');
	int len = -1, z[20]; while (x > 0) z[++len] = x%10, x /= 10;
	for (RG int i = len; i >= 0; i--) putchar(z[i]+48);return ;
}
const int N = 1e5+10, M = 5e5+10;
int h[N];

struct node {
	int a, b, c, id;
	bool operator < (const node & z) const {
		return c < z.c;
	}
}e[M], Q[M];

struct ST_tree {
	int ls, rs, v;
}t[N*20];
int root[N], tot;

void insert(int &now, int l, int r, int k) {
	if (!now) now = ++tot;
	t[now].v++;
	if (l == r) return;
	int mid = (l + r) >> 1;
	if (k <= mid) insert(t[now].ls, l, mid, k);
	else insert(t[now].rs, mid+1, r, k);
}

int query(int rt, int l, int r, int k) {
	if (l == r) return l;
	int mid = (l + r) >> 1, cnt = t[t[rt].ls].v;
	if (k <= cnt) return query(t[rt].ls, l, mid, k);
	return query(t[rt].rs, mid+1, r, k-cnt);
}
int fa[N], siz[N];
int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

int o[N], len, ans[M];

int Merge(int x, int y) {
	if (!x || !y) return x+y;
	t[x].v += t[y].v;
	t[x].ls = Merge(t[x].ls, t[y].ls);
	t[x].rs = Merge(t[x].rs, t[y].rs);
	return x;
}

void merge(int x, int y) {
	x = find(x); y = find(y);
	if (x == y) return ;
	fa[y] = x;
	root[x] = Merge(root[x], root[y]);
	siz[x] += siz[y];
}

int main() {
	int n, m, q, p = 1;
	read(n), read(m), read(q);
	for (int i = 1; i <= n; i++) read(h[i]), fa[i] = i, o[i] = h[i], siz[i] = 1;

	sort(o+1, o+1+n);

	len = unique(o+1, o+1+n) - o - 1;

	for (int i = 1; i <= n; i++) {
		h[i] = lower_bound(o+1, o+1+len, h[i]) - o;
		insert(root[i], 1, len, h[i]);
	}
	for (int i = 1; i <= m; i++)
		read(e[i].a), read(e[i].b), read(e[i].c);
	for (int i = 1; i <= q; i++)
		read(Q[i].a), read(Q[i].c), read(Q[i].b), Q[i].id = i;
	sort(e+1, e+1+m);
	sort(Q+1, Q+1+q);
/*	for (int i = 1; i <= q; i++)
		printf("%d %d %d\n", Q[i].a, Q[i].b, Q[i].c);*/

	for (int i = 1; i <= q; i++) {
		while (p <= m && e[p].c <= Q[i].c) merge(e[p].a, e[p].b), p++;
		if (siz[find(Q[i].a)] < Q[i].b) ans[Q[i].id] = -1;
		else ans[Q[i].id] = o[query(root[find(Q[i].a)], 1, len, siz[find(Q[i].a)]-Q[i].b+1)];
	}
	for (int i = 1; i <= q; i++)
		printf("%d\n", ans[i]);
	return 0;
}

在线算法:主席树+Kruskal重构树

一开始以为加强版是数据加强..

Kruskal重构树

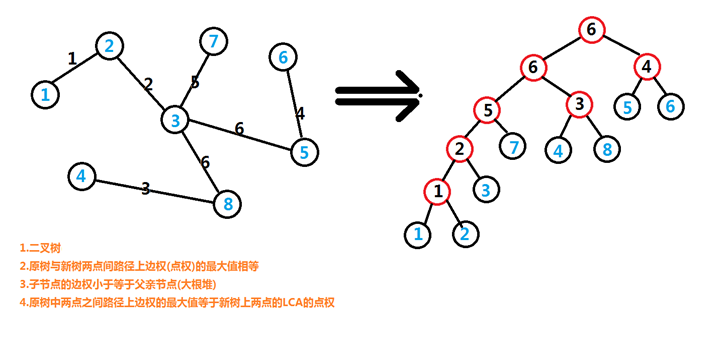
满足堆的性质

所以我们可以倍增找到最大的小于等于一个权值的点

然后它的子树里的所有点都可以互相到达

求第\(k\)大的点,在\(dfs\)序上主席树即可

Code

#include<bits/stdc++.h>

#define LL long long
#define RG register

using namespace std;
template<class T> inline void read(T &x) {
	x = 0; RG char c = getchar(); bool f = 0;
	while (c != '-' && (c < '0' || c > '9')) c = getchar(); if (c == '-') c = getchar(), f = 1;
	while (c >= '0' && c <= '9') x = x*10+c-48, c = getchar();
	x = f ? -x : x;
	return ;
}
template<class T> inline void write(T x) {
	if (!x) {putchar(48);return ;}
	if (x < 0) x = -x, putchar('-');
	int len = -1, z[20]; while (x > 0) z[++len] = x%10, x /= 10;
	for (RG int i = len; i >= 0; i--) putchar(z[i]+48);return ;
}
const int N = 2e5+10, M = 5e5+10;
int n, m, q, h[N];

struct Edge {
	int u, v, w;
	bool operator < (const Edge &z) const {
		return w < z.w;
	}
}e[M];

int fa[N], val[N], tot;
int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}
struct node {
	int to, nxt;
}g[N];
int last[N], gl;
void add(int x, int y) {
	g[++gl] = (node) {y, last[x]};
	last[x] = gl;
}

void kruskal() {
	sort(e+1, e+1+m);
	for (int i = 1; i <= n; i++)
		fa[i] = i;
	int cnt = 0;
	for (int i = 1; i <= m; i++) {
		int u = e[i].u, v = e[i].v, w = e[i].w;
		u = find(u), v = find(v);
		if (u == v) continue;
		h[++tot] = w;
		add(tot, u), add(tot, v);
		fa[u] = fa[v] = fa[tot] = tot;
		if (++cnt == n-1) break;
	}
	return ;
}

int dfn[N], cnt, l[N], r[N];
int anc[N][21];

void dfs(int u) {
	if (u <= n)
		dfn[++cnt] = h[u];
	l[u] = cnt;
	for (int i = 1; i <= 20; i++)
		anc[u][i] = anc[anc[u][i-1]][i-1];
	for (int i = last[u]; i; i = g[i].nxt) {
		int v = g[i].to;
		anc[v][0] = u;
		dfs(v);
	}
	r[u] = cnt;
	return ;
}
int o[N];

struct Tree {
	struct node {
		int ls, rs, v;
	}t[N*20];
	int cnt, root[N];
	void insert(int &now, int l, int r, int pos) {
		t[++cnt] = t[now];
		now = cnt;
		t[now].v++;
		if (l == r) return ;
		int mid = (l + r) >> 1;
		if (pos <= mid) insert(t[now].ls, l, mid, pos);
		else insert(t[now].rs, mid+1, r, pos);
	}
	int query(int rt1, int rt2, int l, int r, int k) {
		if (l == r) return l;
		int mid = (l + r) >> 1, tmp = t[t[rt2].ls].v - t[t[rt1].ls].v;
		if (tmp < k) return query(t[rt1].rs, t[rt2].rs, mid+1, r, k-tmp);
		else return query(t[rt1].ls, t[rt2].ls, l, mid, k);
	}
}T;

int main() {
	read(n), read(m), read(q);
	tot = n;
	for (int i = 1; i <= n; i++) read(h[i]), o[i] = h[i];
	for (int i = 1; i <= m; i++) read(e[i].u), read(e[i].v), read(e[i].w);
	kruskal();
	dfs(tot);
	sort(o+1, o+1+n);
	int K = unique(o+1, o+1+n) - o - 1;
	for (int i = 1; i <= n; i++)
		dfn[i] = lower_bound(o+1, o+1+K, dfn[i]) - o;
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		T.root[i] = T.root[i-1];
		T.insert(T.root[i], 1, K, dfn[i]);
	}
	h[0] = 2147483647;
	while (q--) {
		if (ans == -1) ans = 0;
		int v, x, k; read(v), read(x), read(k);
		v ^= ans, x ^= ans, k ^= ans;
		for (int i = 20; i >= 0; i--)
			if (h[anc[v][i]] <= x) v = anc[v][i];
		if (r[v] - l[v] < k) ans = -1;
		else ans = o[T.query(T.root[l[v]], T.root[r[v]], 1, K, r[v]-l[v]+1-k)];
		write(ans); putchar('\n');
	}
	return 0;
}