Opencv Convex Hull (凸包)

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

Mat img1, img2, img3, img4, img_result, img_gray1, img_gray2, img_gray3, img_canny1;

char win1[] = "window1";
char win2[] = "window2";
char win3[] = "window3";
char win4[] = "window4";
char win5[] = "window5";

int thread_value = 100;
int max_value = 255;
RNG rng1(12345);

int Demo_Convex_Hull();
void Demo_1(int, void*);

//发现凸包
int Demo_Convex_Hull()
{
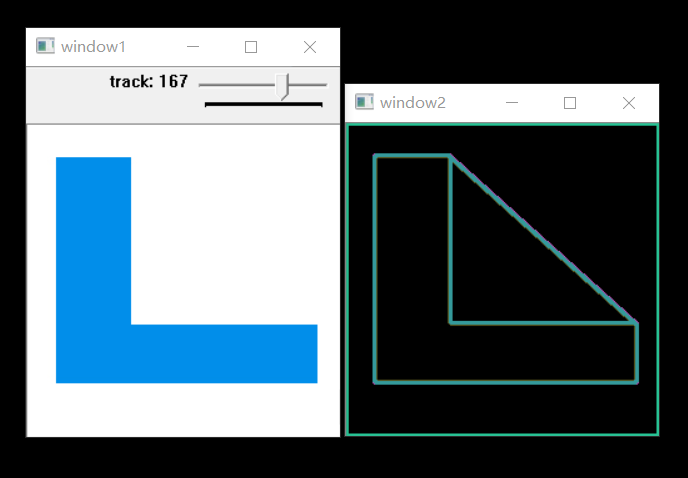
　　namedWindow(win1, CV_WINDOW_AUTOSIZE);
　　namedWindow(win2, CV_WINDOW_AUTOSIZE);
　　//namedWindow(win3, CV_WINDOW_AUTOSIZE);

　　img1 = imread("D://images//1//temp2.jpg");
　　//img2 = imread("D://images//1//p5_1.jpg");
　　if (img1.empty())
　　{
　　　　cout << "could not load image..." << endl;
　　　　return 0;
　　}

　　imshow(win1, img1);
　　img4 = Mat::zeros(img1.size(),CV_8UC3);

　　//转灰度图
　　cvtColor(img1, img_gray1, CV_BGR2GRAY);
　　//模糊处理
　　blur(img_gray1, img2, Size(3, 3), Point(-1, -1),BORDER_DEFAULT);

　　createTrackbar("track", win1, &thread_value, max_value, Demo_1);
　　Demo_1(0,0);

　　return 0;
}

void Demo_1(int,void*)
{
　　vector<vector<Point>> vec_p;
　　vector<Vec4i> vec_4i;

　　threshold(img2, img3, thread_value, max_value, THRESH_BINARY);
　　findContours(img3, vec_p, vec_4i, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0));

　　vector<vector<Point>> convexs(vec_p.size());
　　for (size_t i=0;i<vec_p.size();i++)
　　{
　　　　convexHull(vec_p[i], convexs[i], false, true);
　　}

　　for (size_t j=0;j<vec_p.size();j++)
　　{
　　　　Scalar color_1 = Scalar(rng1.uniform(0,255), rng1.uniform(0, 255), rng1.uniform(0, 255));
　　　　drawContours(img4, vec_p, j, color_1, 2, LINE_8, vec_4i, 0, Point(0, 0));
　　　　drawContours(img4, convexs, j, color_1, 2, LINE_8, vec_4i, 0, Point(0, 0));
　　}
　　imshow(win2,img4);
}

int main()
{
　　Demo_Convex_Hull();

　　waitKey(0);
　　return 0;
}