2017-2018-1 20179202《Linux内核原理与分析》第二周作业

本周着重学习了汇编指令，并通过反汇编C程序了解栈帧变化。

实践

看了孟老师的演示视频后，我重新写了C程序，如下：

 int main()
{
    int a=1,b=2;
    return g(a,b);
 }
 int g(int x,int y)
 {
    return x+y;
 }

通过 gcc –S –o main.s main.c -m32反汇编，删除不需要的信息：

main:
	pushl	%ebp
	movl	%esp, %ebp
	andl	$-16, %esp
	subl	$32, %esp
	movl	$1, 24(%esp)
	movl	$2, 28(%esp)
	movl	28(%esp), %eax
	movl	%eax, 4(%esp)
	movl	24(%esp), %eax
	movl	%eax, (%esp)
	call	g
	leave
	ret
g:
	pushl	%ebp
	movl	%esp, %ebp
	movl	12(%ebp), %eax
	movl	8(%ebp), %edx
	addl	%edx, %eax
	popl	%ebp
	ret

在分析汇编程序执行的过程时，我想对自己的分析进行验证（例如每一步是否esp,ebp所在位置是否与我分析的一致），于是我想到了用调试的方法。在阅读课本18章时我知道了调试需要使用gdb。通过 gcc –g –o main main.s -m32生成main可执行程序，然后开始调试：

可以看出ebp值为0x0，esp值为0xffffd4ac，eip值为0x80483ed，是main函数的第一条指令pushl %ebp，初始栈空间大致如下：

执行以下两条指令：

pushl	%ebp
movl	%esp, %ebp

此时ebp和esp的值均为0xffffd4a8，存放的是ebp原来的值0x00000000，栈空间大致如下：

andl	$-16, %esp

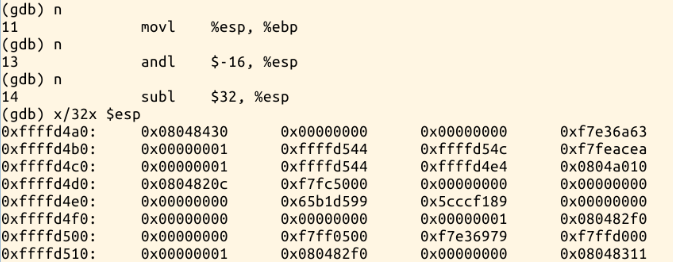
可以看出esp减少了8个字节，栈空间大致如下：

subl $32, %esp为局部变量预留空间，栈空间如下：

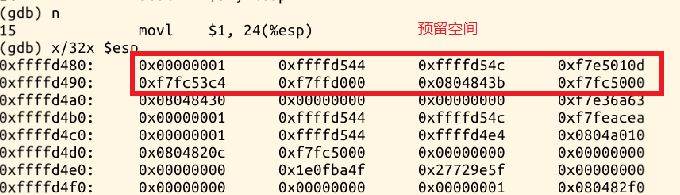
movl	$1, 24(%esp)
movl	$2, 28(%esp)
movl	28(%esp), %eax
movl	%eax, 4(%esp)
movl	24(%esp), %eax
movl	%eax, (%esp)

将1，2分别放到esp指地址向高地址分别偏移24、28个字节处，再将其分别赋给eax,eax再将值放到esp指地址向高地址偏移4个字节以及esp所指地址处（注：esp值没有变），栈空间大致如下：

**思考：

（1）此处为什么要把1和2两次存入空间？**

我将原代码改为：

 int main()
{
    int a=1,b=2;
    return a+b;
 }

编译后：

去掉函数调用后，确实少了参数第二次入栈，这让我想到了函数调用中的实参和形参，第二次入栈的可能是形参x和y，但现在还不能确定（后面的分析可以解决）。

（2）第二次入栈中，为什么先入“2”后入“1”？

   参考为什么函数入栈顺序从右往左

call指令将下一条要执行的leave指令的地址0x0804841a压入栈,esp加4值为0xffffd47c,调试结果及栈空间如下：

进入g函数，前两条指令同上，即将旧的ebp压入栈，并将ebp移到esp所指位置：

movl	12(%ebp), %eax
movl	8(%ebp), %edx
addl	%edx, %eax

三条指令完成了1+2，此时eax里的值为3：

这里所使用的“1”和“2”是8(%ebp)和12(%ebp)中的，即是第二次入栈的，它们参与的是g函数的运算，因此可以确定二者是形参。

popl %ebp 指令执行后，恢复ebp，此时esp的值为main函数的leave指令:

ret相当于执行popl %eip,从g函数返回main函数：

leave指令相当于

movl %ebp,%esp popl %ebp

ret后：

附表（每一条指令执行后eip，ebp，esp，eax，edx的值）：

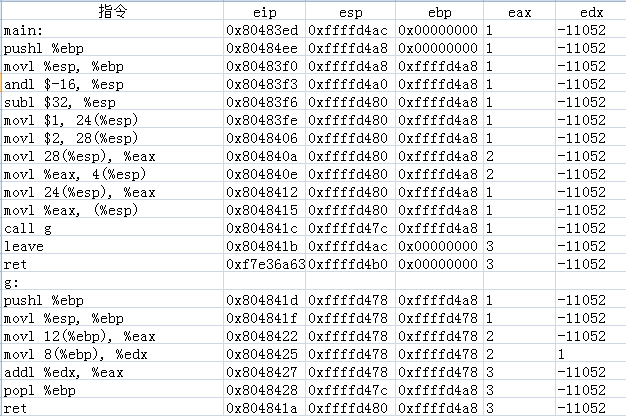
操作结束后我发现很多函数调用中都有leave指令，自己实践的g函数却没有，那是怎么回到main函数的呢？分析后我发现g函数没有增加变量，所以不用再次分配空间，ebp和esp所指位置相同，这和增加变量后分配空间，用leave指令的第一步movl %ebp,%esp 将esp移回栈顶同理，故g函数只有leave指令的第二步。这加深了我对leave指令的理解，既然分配空间要用leave，那leave指令便有将栈中为函数预留空间“收回”的功能。

未解决问题

  经过搜索后知道andl $-16, %esp命令是为了实现地址对齐的填充数据，但为什么在实践中esp减少了8个字节而不是16个字节？

小结

1.通过本周学习，对本科所学的数据结构中的栈有了更深刻的认识，每个栈帧对应着一个未运行完的函数，栈帧中保存了该函数的返回地址和局部变量；

2.以前学习C语言只知道写出程序能够实现功能就可以了，现在初步了解写出的语言转化为汇编语言如何在计算机中运行（如：实参、形参、返回、调用到底如何实现）；

3.计算机体系结构中的中断时保存现场和pushl $eip有异曲同工之处。