Deep Learning入门

今天在看电影的过程中我忽然想起来几件特别郁闷的事，我居然忘了上周三晚上的计算机接口的实验课！然后我又想起来我又忘了上周六晚上的就业指导！
然后一阵恐惧与责备瞬间涌了上来。
这事要是在以前我绝对会释然的，可是重要的事说三遍~我要保研，我要保研，我要保研！我怎么能这么大意啊！！！！！！！！！！
哎，郁闷，还是说说代码吧。
心情不好转移一下
　　　　　　　　　　　　　　　　　　　　　　　　　　　郁闷的分割线

---

学习此内容是建立在文本分类的MaxEntSentiment最大熵分类的基础上的，代码可以在github下载

稀疏特征构成单层神经网络

什么是稀疏特征

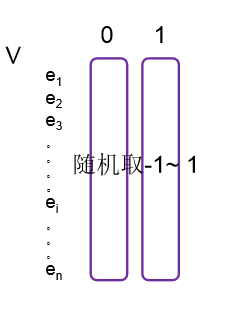
所谓稀疏特征就是说，在整个特征库V中选中的特征是很少的（如果说选中的特征用1标记，没选中的特征用0标记）
那么在整个特征向量中（0的个数大于1的个数）

比如说一个特征库中有A,B,C,D,E,F,G,H,I。。。。Z 26个特征 现在有一个句子中有A B C D这个四个特征 ，那么就表示为（1,1,1,1,0,0,0,0,0,0,0,0….）
可以参考:https://www.zhihu.com/question/31951092

单层神经网络

单层神经网络就是只有一个隐层
现在我们的目的是来判断一个句子是正向的还是负向的

第一步：

就是去特征库中找到想要的特征
比如：(就是含有特征A，B，C，D的这个句子)x:（1,1,1,1,0,0,0,0,0,0,0,0….）

第二步：

构建一个26*2（第一个参数是你有多少特征，第二个参数是你要分几类。前面的例子是由26个特征，要分为2类，正向1，负向0）的特征库，每一行表示这个特征在正向和负向上的“贡献”，就是这个特征有多大可能是正向的，多大可能是负向的。
当然，我们不会手工的对这26个特征进行正向和负向的赋值。因为深度学习是要学习的吗。所以最开始给他们赋值为-1到1的随机数

第三步：

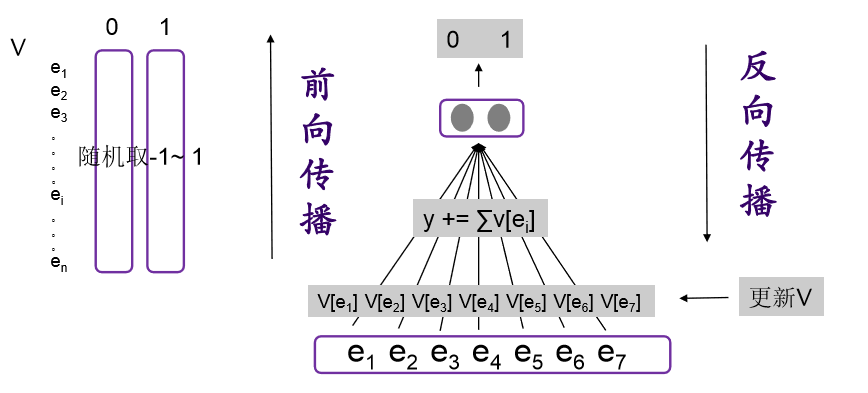
V与x这两个矩阵相乘，x是1*26的，V是2*62的 结果就是1*2的矩阵。
也可以换种角度思考：对所选中的特征在0那一列的数值加一起，然后在1那一列的数值在一起。最后也是1*2的矩阵。有人说，这不是废话么。。。但是在编程的时候就不用乘了，直接加就可了，提高了速度？？代码中就是这么定义的V，这么定义的目的就是在前向计算的时候是把这个矩阵出现的特征0， 1向分别加一起而不是v乘x

再提一句什么是前向计算：ComputeForward
v*x就是前向计算啦~~~ 我觉得这个名字就是为了一会要出现的反向计算而起的名字。这个12的矩阵就是最后的输出y ()

第四步：

这个1*2的矩阵我们还要变个形下，对她进行归一化也就是softmax。
可以这么想，想要统计理科的分数和100分有多大差距，你是不是要把你理科成绩加一起然后再除以科目数吧，这样你才能和100分对比。这里的softmax是不是类似这个功能。

第五步：

和真实情况对比求差距。产生差距的原因可定是每一个特征对正向和负向的赋值不准确。
然后反过来改v。这个就叫ComputeBackward。反向计算

---

然后再继续回到第三步。。。反复。。。。

这里的e1 e2神马的 就是所选择的特征，这个图中是选择了7个特征。然后在V中把它们正向和负向分别加一起（y是1*2的矩阵）与0,1做对比。这里的隐层就是图片中灰色的V

这个是学长做的图片，我就直接拿来了，我有空会自己做一个我自己觉得好理解的图片的。
单层的就说完了
下一篇讲多层的，和它几乎一样。我会尽量更详细的用图来解释，以及对这里有些一带而过的ComputeBackward进一步说明

---

22点45了。哎~早点睡觉明天早点起来去占个座，不能再继续这样不积极了。连课都会忘了，也不认真听课！大三下加油！

---

　　　　　　　　　　　　　　　　　　　　　郁闷的结束线

坚持是一种伟大的力量，可以改变一切

​