Python Seaborn 笔记

Seaborn是Python的一个制图工具库，在Matplotlib上构建，支持numpy和pandas的数据结构可视化。

他有多个内置的主题，颜色的主题

可视化单一变量，二维变量用于比较各个变量的分布情况

可视化线性回归模型中的独立变量以及不独立变量

可视化矩阵数据，通过聚类算法探索矩阵间的结构

可视化时间序列数据以及不确定性的展示

可在分割区域制图，用于复杂的可视化

Seaborn还是比较简单的，看看文档基本就可以写了。

bins : argument for matplotlib hist(), or None, optional #设置矩形图数量 Specification of hist bins, or None to use Freedman-Diaconis rule.

hist : bool, optional #控制是否显示条形图 Whether to plot a (normed) histogram.

kde : bool, optional #控制是否显示核密度估计图 Whether to plot a gaussian kernel density estimate.

rug : bool, optional #控制是否显示观测的小细条（边际毛毯）Whether to draw a rugplot on the support axis.

fit : random variable object, optional #控制拟合的参数分布图形 An object with fit method, returning a tuple that can be passed to a pdf method a positional arguments following an grid of values to evaluate the pdf on.

{hist, kde, rug, fit}_kws : dictionaries, optional Keyword arguments for underlying plotting functions.

vertical : bool, optional #显示正交控制 If True, oberved values are on y-axis.

单变量分布

import numpy as np
import seaborn as sns

x1 = np.random.normal(size=500)
# 直方图
sns.distplot(x1, bins=20, kde=False, rug=True)

　

# 核密度估计
sns.distplot(x1, hist=False, rug=True)

　　

# 拟合参数分布
sns.distplot(x1, kde=True, fit=stats.gamma)

　

双变量分布

df_obj2 = pd.DataFrame({"x": np.random.randn(500),"y": np.random.randint(0, 100, 500)})
# 散布图
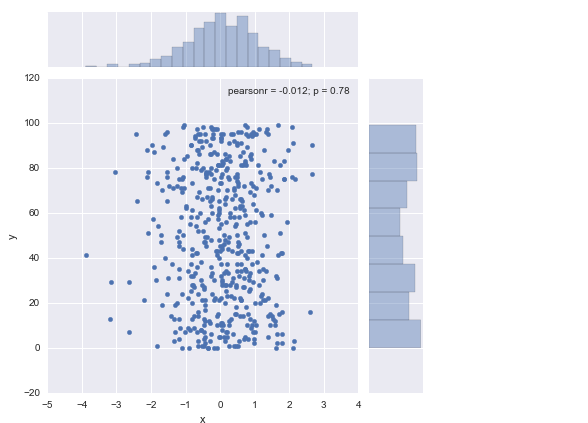
sns.jointplot(x="x", y="y", data=df_obj2)

　　

# 二维直方图
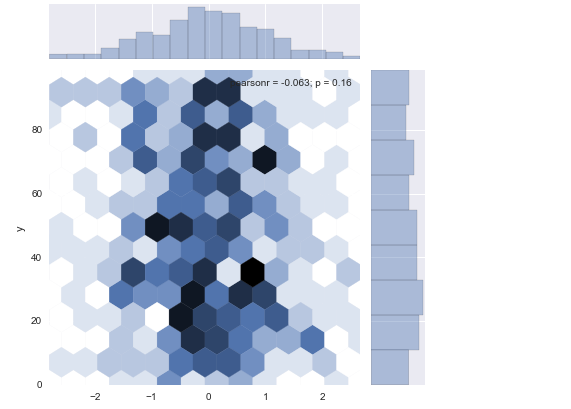
sns.jointplot(x="x", y="y", data=df_obj2, kind="hex");

　　

# 核密度估计
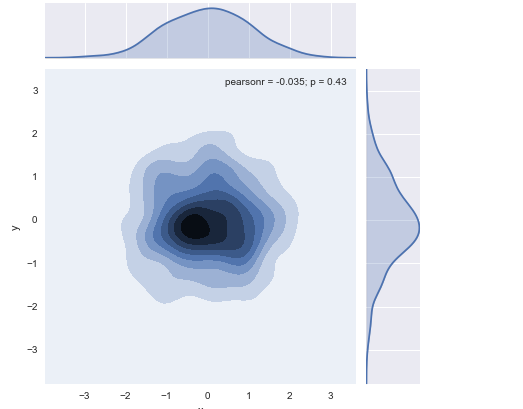
sns.jointplot(x="x", y="y", data=df_obj1, kind="kde");

　　

# 数据集中变量间关系可视化
dataset = sns.load_dataset("tips")
#dataset = sns.load_dataset("iris")
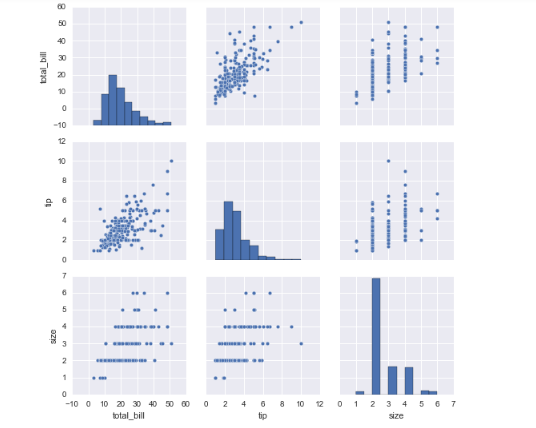
sns.pairplot(dataset);

　　

类别数据可视化

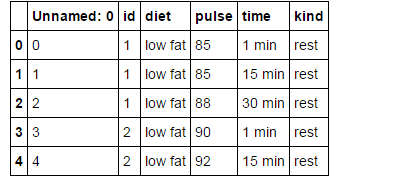
exercise = sns.load_dataset('exercise')
exercise.head(5)
sns.stripplot(x="diet", y="pulse", data=exercise)
sns.swarmplot(x="diet", y="pulse", data=exercise, hue='kind') #hue按照组类别

　　

　

# 盒子图
sns.boxplot(x="diet", y="pulse", data=exercise)
#sns.boxplot(x="diet", y="pulse", data=exercise, hue='kind')
# 小提琴图
#sns.violinplot(x="diet", y="pulse", data=exercise)
sns.violinplot(x="diet", y="pulse", data=exercise, hue='kind')
# 柱状图
sns.barplot(x="diet", y="pulse", data=exercise, hue='kind')
# 点图
sns.pointplot(x="diet", y="pulse", data=exercise, hue='kind')