NOIP2013 提高组 Day2

期望得分：100+100+30+=230+

实际得分：100+70+30=200

T2 觉得题目描述有歧义：

若存在2i却不存在2i+1，自己按不合法做的，实际是合法的

T3 bfs 难以估分

虽然得了30，但代码有bug，debug后50

https://www.luogu.org/problem/lists?name=&orderitem=pid&tag=83%7C30

T1 积木大赛

题目描述

春春幼儿园举办了一年一度的“积木大赛”。今年比赛的内容是搭建一座宽度为n的大厦，大厦可以看成由n块宽度为1的积木组成，第i块积木的最终高度需要是hi。

在搭建开始之前，没有任何积木（可以看成n块高度为 0 的积木）。接下来每次操作，小朋友们可以选择一段连续区间[l, r]，然后将第第 L 块到第 R 块之间（含第 L 块和第 R 块）所有积木的高度分别增加1。

小 M 是个聪明的小朋友，她很快想出了建造大厦的最佳策略，使得建造所需的操作次数最少。但她不是一个勤于动手的孩子，所以想请你帮忙实现这个策略，并求出最少的操作次数。

输入输出格式

输入格式：

输入文件为 block.in

输入包含两行，第一行包含一个整数n，表示大厦的宽度。

第二行包含n个整数，第i个整数为hi 。

输出格式：

输出文件为 block.out

仅一行，即建造所需的最少操作数。

输入输出样例

输入样例#1：

5

2 3 4 1 2

输出样例#1：

说明

【样例解释】

其中一种可行的最佳方案，依次选择

[1,5] [1,3] [2,3] [3,3] [5,5]

【数据范围】

对于 30%的数据，有1 ≤ n ≤ 10；

对于 70%的数据，有1 ≤ n ≤ 1000；

对于 100%的数据，有1 ≤ n ≤ 100000，0 ≤ hi≤ 10000。

将积木的高度用点、线画出来

对于每一段上凸的部分，所需操作次数是它的最大值 - 前一段上凸部分的最右端

#include<cstdio>

#define N 100011

using namespace std;

int n,a[N];

struct node

{

    int high,end;

}e[N];

int cnt,ans;

bool up;

int main()

{

    /*freopen("BlockNOIP2013.in","r",stdin);

    freopen("BlockNOIP2013.out","w",stdout);*/

    scanf("%d",&n);

    for(int i=;i<=n+;i++)

    {

        if(i<=n) scanf("%d",&a[i]);

        if(!up&&a[i]>a[i-])

        {

            e[cnt].end=a[i-];

            up=true;

            cnt++;

        }

        else if(up&&a[i]<a[i-])

        {

            e[cnt].high=a[i-];

            up=false;

        }

    }

    ans=e[].high;

    for(int i=;i<=cnt;i++) ans+=e[i].high-e[i-].end;

    printf("%d",ans);

}

T2 花匠

题目描述

花匠栋栋种了一排花，每株花都有自己的高度。花儿越长越大，也越来越挤。栋栋决定

把这排中的一部分花移走，将剩下的留在原地，使得剩下的花能有空间长大，同时，栋栋希

望剩下的花排列得比较别致。

具体而言，栋栋的花的高度可以看成一列整数h1,h2..hn。设当一部分花被移走后，剩下的花的高度依次为g1,g2..gn，则栋栋希望下面两个条件中至少有一个满足：

条件 A：对于所有g(2i)>g(2i-1),g(2i)>g(2i+1)

条件 B：对于所有g(2i)<g(2i-1),g(2i)<g(2i+1)

注意上面两个条件在m = 1时同时满足，当m > 1时最多有一个能满足。

请问，栋栋最多能将多少株花留在原地。

输入输出格式

输入格式：

输入文件为 flower .in。

输入的第一行包含一个整数n，表示开始时花的株数。

第二行包含n个整数，依次为h1,h2..hn,表示每株花的高度。

输出格式：

输出文件为 flower .out。

输出一行，包含一个整数m，表示最多能留在原地的花的株数。

输入输出样例

输入样例#1：

5

5 3 2 1 2

输出样例#1：

说明

【输入输出样例说明】

有多种方法可以正好保留 3 株花，例如，留下第 1、4、5 株，高度分别为 5、1、2，满

足条件 B。

【数据范围】

对于 20%的数据，n ≤ 10；

对于 30%的数据，n ≤ 25；

对于 70%的数据，n ≤ 1000，0 ≤ ℎi≤ 1000；

对于 100%的数据，1 ≤ n ≤ 100,000，0 ≤ hi≤ 1,000,000，所有的hi 随机生成，所有随机数服从某区间内的均匀分布。

将花的高度用电、线画出来

最大保留值=拐点+1

第一个点开始先向上还是先向下分开算

#include<cstdio>

#include<algorithm>

using namespace std;

int n,a[];

bool up;

int ans1,ans2;

int main()

{

    scanf("%d",&n);

    for(int i=;i<=n;i++) scanf("%d",&a[i]);

    a[]=0x7fffffff;

    for(int i=;i<=n;i++)

    {

        if(!up&&a[i]>a[i-])

        {

            ans1++;

            up=true;

        }

        else if(up&&a[i]<a[i-])

        {

            ans1++;

            up=false;

        }

    }

    up=true;

    a[]=-;

    for(int i=;i<=n;i++)

    {

        if(up&&a[i]<a[i-])

        {

            ans2++;

            up=false;

        }

        else if(!up&&a[i]>a[i-])

        {

            ans2++;

            up=true;

        }

    }

    printf("%d",max(ans1,ans2)+);

}

T3 华容道

题目描述

【问题描述】

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；
有些棋子是固定的，有些棋子则是可以移动的；
任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次

玩的时候，空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi列，目标位置为第 TXi 行第 TYi 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入输出格式

输入格式：

输入文件为 puzzle.in。

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式：

输出文件名为 puzzle.out。

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

输入输出样例

输入样例#1：

3 4 2

0 1 1 1

0 1 1 0

0 1 0 0

3 2 1 2 2 2

1 2 2 2 3 2

输出样例#1：

2

-1

说明

【输入输出样例说明】

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

移动过程如下：

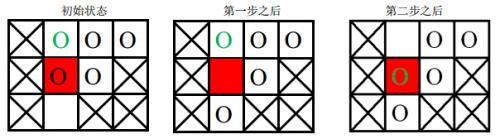
第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

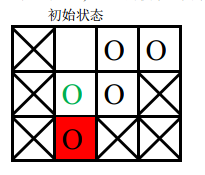
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无

法完成。

【数据范围】

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；

对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；

对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

50分暴力法：

bfs跟踪空白块，找所有的可移动的方案，直至到达目标状态

bfs判重方式：将整个棋盘转化为字符串

发现，若空白块与指定块都在同一位置，其他的可移动的块无论怎么移，都是没用的

所以只需要记录空白块与指定块的位置，就够了

所以80分暴力法：

bfs跟踪空白块，找所有的可移动的方案，直至到达目标状态

bfs判重方式：用mp[i][j][k][l]表示空白块在（i，j），指定块在（k，l）

它的局限性在于

搜索是盲目的，产生大量无用状态

进一步思考，

只有空白块与指定块相邻时，状态才是有用的

所以，由此得出AC做法：

1、预处理所有的有用状态

对于1个指定块和一个空白块，有4种有效状态：空白块分别在指定块的上、下、左、右

对于每一种有效状态，有4种后继状态：另外3个方向的状态、交换空白块与指定块

枚举每一个指定块、再枚举指定块的每一个有效状态，bfs计算到每一个后继状态的最小步数

由有效状态向后继状态连权值为最小步数的边

这样我们就构出了一张图

2、对于每一个初始局面，bfs 算出空白块与指定块之间有效状态的步数

也就是算出空白块移到指定块四周的步数

3、将第2步算出的结果作为初始值，在第1步构出的图中跑最短路

如何简介的表示状态？

我的方法；

用0,1,2,3分别表示上右下左

状态=（（行号-1）*列数+（列号-1））*4+ 0/1/2/3

看不懂的话，带两个格的8种有效状态手算

由此可得，不断的减少状态数，是优化bfs的一种方法

AC代码：

#include<iostream>

#include<cstring>

#include<cstdio>

#include<queue>

using namespace std;

int n,m,p;

bool a[][],v[];

int x[]={-,,,};

int y[]={,,,-};

int pre_dis[][],dis[];

int front[],to[*],nextt[*],w[*],tot;

void add(int u,int v,int val)

{

    to[++tot]=v; nextt[tot]=front[u]; front[u]=tot; w[tot]=val;

}

struct node

{

    int x,y;

}nxt,cur;

queue<node>q;

queue<int>k;

int turn(int i,int j)

{

    return (i-)*m+j-<<;

}

void bfs(int ex,int ey,int px,int py,int d)

{

    int cx,cy,nx,ny;

    memset(pre_dis,-,sizeof(pre_dis));

    pre_dis[px][py]=; pre_dis[ex][ey]=;

    cur.x=ex;cur.y=ey;

    q.push(cur);

    while(!q.empty())

    {

        cur=q.front(); q.pop();

        cx=cur.x,cy=cur.y;

        for(int i=;i<;i++)

        {

            nx=cur.x+x[i],ny=cur.y+y[i];

            if(a[nx][ny]&&pre_dis[nx][ny]==-)

            {

                pre_dis[nx][ny]=pre_dis[cx][cy]+;

                nxt.x=nx; nxt.y=ny;

                q.push(nxt);

            }

        }

    }

    if(d==) return;

    int tmp=turn(px,py);

    for(int i=;i<;i++)

        if(pre_dis[px+x[i]][py+y[i]]>) add(tmp+d,tmp+i,pre_dis[px+x[i]][py+y[i]]);

    add(tmp+d,turn(ex,ey)+(d+)%,);

}

void spfa(int sx,int sy)

{

    int tmp;

    memset(dis,-,sizeof(dis));

    for(int i=;i<;i++)

     if(pre_dis[sx+x[i]][sy+y[i]]!=-)

     {

         tmp=turn(sx,sy)+i;

         dis[tmp]=pre_dis[sx+x[i]][sy+y[i]];

         k.push(tmp);

     }

    int now;

    while(!k.empty())

    {

        now=k.front();

        k.pop();

        v[now]=false;

        for(int i=front[now];i;i=nextt[i])

            if(dis[to[i]]==-||dis[to[i]]>dis[now]+w[i])

            {

                dis[to[i]]=dis[now]+w[i];

                if(!v[to[i]])

                {

                    v[to[i]]=true;

                    k.push(to[i]);

                }

            }

    }

}

int main()

{

    scanf("%d%d%d",&n,&m,&p);

    for(int i=;i<=n;i++)

     for(int j=;j<=m;j++)

               scanf("%d",&a[i][j]);

    for(int i=;i<=n;i++)

     for(int j=;j<=m;j++)

      if(a[i][j])

      {

         if(a[i-][j]) bfs(i-,j,i,j,);

         if(a[i][j+]) bfs(i,j+,i,j,);

         if(a[i+][j]) bfs(i+,j,i,j,);

         if(a[i][j-]) bfs(i,j-,i,j,);

      }

    int ex,ey,sx,sy,tx,ty,ans;

    while(p--)

    {

        scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);

        if(sx==tx&&sy==ty)

        {

            printf("0\n");

            continue;

        }

        bfs(ex,ey,sx,sy,);

        spfa(sx,sy);

        ans=0x7fffffff; int tmp=turn(tx,ty);

        for(int i=;i<;i++)

         if(dis[tmp+i]!=-) ans=min(ans,dis[tmp+i]);

        if(ans==0x7fffffff) ans=-;

        printf("%d\n",ans);

    }

}

80分暴力代码：（洛谷上70）

#include<iostream>

#include<cstring>

#include<cstdio>

#include<queue>

using namespace std;

int n,m,p;

bool a[][],mp[][][][];

int ex,ey,sx,sy,tx,ty;

int cx,cy,nx,ny;

int x[]={-,,,};

int y[]={,,,-};

struct node

{

    int emx,emy,stx,sty,step;

}cur,nxt;

queue<node>q;

void bfs()

{

    while(!q.empty()) q.pop();

    cur.emx=ex; cur.emy=ey; cur.step=;

    cur.stx=sx; cur.sty=sy;

    q.push(cur);

    while(!q.empty())

    {

        cur=q.front(); q.pop();

        cx=cur.emx; cy=cur.emy;

        for(int i=;i<;i++)

        {

            nx=cx+x[i]; ny=cy+y[i];

            if(a[nx][ny])

            {

                if(nx==cur.stx&&ny==cur.sty) nxt.stx=cur.emx,nxt.sty=cur.emy;

                else nxt.stx=cur.stx,nxt.sty=cur.sty;

                if(nxt.stx==tx&&nxt.sty==ty)

                {

                    printf("%d\n",cur.step+);

                    return;

                }

                if(!mp[nx][ny][nxt.stx][nxt.sty])

                {

                    mp[nx][ny][nxt.stx][nxt.sty]=true;

                    nxt.emx=nx; nxt.emy=ny;

                    nxt.step=cur.step+;

                    q.push(nxt);

                }

            }

        }

    }

    printf("-1\n");

    return;

}

int main()

{

    freopen("PuzzleNOIP2013.in","r",stdin);

    freopen("PuzzleNOIP2013.out","w",stdout);

    scanf("%d%d%d",&n,&m,&p);

    for(int i=;i<=n;i++)

     for(int j=;j<=m;j++)

               scanf("%d",&a[i][j]);

    while(p--)

    {

        scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);

        if(sx==tx&&sy==ty)

        {

            printf("0\n");

            continue;

        }

        memset(mp,,sizeof(mp));

        mp[ex][ey][sx][sy]=true;

        bfs();

    }

}

50分暴力代码：

#include<iostream>

#include<cstring>

#include<cstdio>

#include<queue>

#include<map>

using namespace std;

int n,m,p;

bool a[][];

int ex,ey,sx,sy,tx,ty,d1,d2;

string s,tmp;

int cx,cy,nx,ny;

int x[]={-,,,};

int y[]={,,,-};

struct node

{

    string k;

    int x,y,step;

}cur,nxt;

queue<node>q;

map<string,bool>mp;

int turn(int i,int j)

{

    return (i-)*m+j-;

}

void bfs()

{

    mp.clear();

    while(!q.empty()) q.pop();

    cur.k=s; cur.x=ex; cur.y=ey; cur.step=;

    q.push(cur);

    mp[s]=true;

    while(!q.empty())

    {

        cur=q.front(); q.pop();

        cx=cur.x; cy=cur.y;

        for(int i=;i<;i++)

        {

            nx=cx+x[i]; ny=cy+y[i];

            if(a[nx][ny])

            {

                d1=turn(cx,cy); d2=turn(nx,ny);

                if(cx==tx&&cy==ty&&cur.k[turn(nx,ny)]=='')

                {

                    printf("%d\n",cur.step+);

                    return;

                }

                swap(cur.k[d1],cur.k[d2]);

                if(!mp[cur.k])

                {

                    nxt.k=cur.k;

                    mp[nxt.k]=true;

                    nxt.x=nx; nxt.y=ny;

                    nxt.step=cur.step+;

                    q.push(nxt);

                }

                swap(cur.k[d1],cur.k[d2]);

            }

        }

    }

    printf("-1\n");

    return;

}

int main()

{

    freopen("PuzzleNOIP2013.in","r",stdin);

    freopen("PuzzleNOIP2013.out","w",stdout);

    scanf("%d%d%d",&n,&m,&p);

    for(int i=;i<=n;i++)

     for(int j=;j<=m;j++)

       {

               scanf("%d",&a[i][j]);

               if(a[i][j]) tmp+='';

               else tmp+='';

       }

    while(p--)

    {

        s=tmp;

        scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);

        s[turn(ex,ey)]='';

        s[turn(sx,sy)]='';

        bfs();

    }

}

开始的时候写得50分暴力，

只得30分，因为bfs到达目标状态后返回主函数，此时队列里可能还未清空

下一次使用这个队列的时候出错

80分暴力开始得60,

原因：代码不能处理指定块就是目标块的情况