HDU - 6172:Array Challenge (BM线性递推)

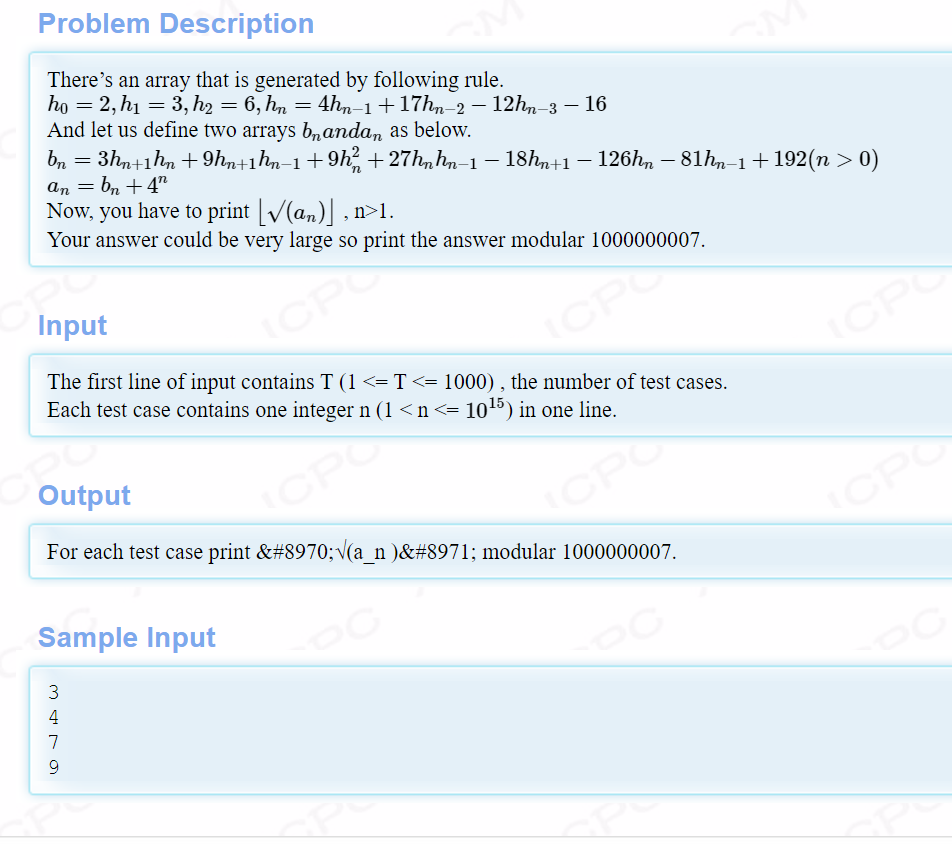
题意：给出，三个函数，h，b，a，然后T次询问，每次给出n，求sqrt(an);

思路：不会推，但是感觉a应该是线性的，这个时候我们就可以用BM线性递推，自己求出前几项，然后放到模板里，就可以求了。

数据范围在1e15，1000组都可以秒过。

（

那么主要的问题就是得确保是线性的，而且得求出前几项。

如果是K<1e6次多项式，我们可以用拉格朗日插值法求第N项，比如求K次方的前缀和，先放着，有空以启整理了。

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=;
ll powmod(ll a,ll b) {ll res=;a%=mod; assert(b>=); for(;b;b>>=){if(b&)res=res*a%mod;a=a*a%mod;}return res;}

ll n;
namespace linear_seq {
    const int N=;
    ll res[N],base[N],_c[N],_md[N];

    vector<int> Md;
    void mul(ll *a,ll *b,int k) {
        rep(i,,k+k) _c[i]=;
        rep(i,,k) if (a[i]) rep(j,,k) _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
        for (int i=k+k-;i>=k;i--) if (_c[i])
            rep(j,,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
        rep(i,,k) a[i]=_c[i];
    }
    int solve(ll n,VI a,VI b) {
        ll ans=,pnt=;
        int k=SZ(a);
        assert(SZ(a)==SZ(b));
        rep(i,,k) _md[k--i]=-a[i];_md[k]=;
        Md.clear();
        rep(i,,k) if (_md[i]!=) Md.push_back(i);
        rep(i,,k) res[i]=base[i]=;
        res[]=;
        while ((1ll<<pnt)<=n) pnt++;
        for (int p=pnt;p>=;p--) {
            mul(res,res,k);
            if ((n>>p)&) {
                for (int i=k-;i>=;i--) res[i+]=res[i];res[]=;
                rep(j,,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
            }
        }
        rep(i,,k) ans=(ans+res[i]*b[i])%mod;
        if (ans<) ans+=mod;
        return ans;
    }
    VI BM(VI s) {
        VI C(,),B(,);
        int L=,m=,b=;
        rep(n,,SZ(s)) {
            ll d=;
            rep(i,,L+) d=(d+(ll)C[i]*s[n-i])%mod;
            if (d==) ++m;
            else if (*L<=n) {
                VI T=C;
                ll c=mod-d*powmod(b,mod-)%mod;
                while (SZ(C)<SZ(B)+m) C.pb();
                rep(i,,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                L=n+-L; B=T; b=d; m=;
            } else {
                ll c=mod-d*powmod(b,mod-)%mod;
                while (SZ(C)<SZ(B)+m) C.pb();
                rep(i,,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                ++m;
            }
        }
        return C;
    }
    int gao(VI a,ll n) {
        VI c=BM(a);
        c.erase(c.begin());
        rep(i,,SZ(c)) c[i]=(mod-c[i])%mod;
        return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
    }
};

int main() {
    int T; scanf("%d",&T);
    while(T--){
        scanf("%lld",&n);
        printf("%lld\n", linear_seq::gao(VI{,,,,,,,,,,},n-))
;
    }
}
//

再比如HDU6185，很显然是线性的，用16*16的矩阵来做会T，我可以用状压DP暴力求出前几项，然后套这个。

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=;
ll powmod(ll a,ll b) {ll res=;a%=mod; assert(b>=); for(;b;b>>=){if(b&)res=res*a%mod;a=a*a%mod;}return res;}

ll _,n;
namespace linear_seq {
    const int N=;
    ll res[N],base[N],_c[N],_md[N];

    vector<int> Md;
    void mul(ll *a,ll *b,int k) {
        rep(i,,k+k) _c[i]=;
        rep(i,,k) if (a[i]) rep(j,,k) _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
        for (int i=k+k-;i>=k;i--) if (_c[i])
            rep(j,,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
        rep(i,,k) a[i]=_c[i];
    }
    int solve(ll n,VI a,VI b) {
        ll ans=,pnt=;
        int k=SZ(a);
        assert(SZ(a)==SZ(b));
        rep(i,,k) _md[k--i]=-a[i];_md[k]=;
        Md.clear();
        rep(i,,k) if (_md[i]!=) Md.push_back(i);
        rep(i,,k) res[i]=base[i]=;
        res[]=;
        while ((1ll<<pnt)<=n) pnt++;
        for (int p=pnt;p>=;p--) {
            mul(res,res,k);
            if ((n>>p)&) {
                for (int i=k-;i>=;i--) res[i+]=res[i];res[]=;
                rep(j,,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
            }
        }
        rep(i,,k) ans=(ans+res[i]*b[i])%mod;
        if (ans<) ans+=mod;
        return ans;
    }
    VI BM(VI s) {
        VI C(,),B(,);
        int L=,m=,b=;
        rep(n,,SZ(s)) {
            ll d=;
            rep(i,,L+) d=(d+(ll)C[i]*s[n-i])%mod;
            if (d==) ++m;
            else if (*L<=n) {
                VI T=C;
                ll c=mod-d*powmod(b,mod-)%mod;
                while (SZ(C)<SZ(B)+m) C.pb();
                rep(i,,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                L=n+-L; B=T; b=d; m=;
            } else {
                ll c=mod-d*powmod(b,mod-)%mod;
                while (SZ(C)<SZ(B)+m) C.pb();
                rep(i,,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                ++m;
            }
        }
        return C;
    }
    int gao(VI a,ll n) {
        VI c=BM(a);
        c.erase(c.begin());
        rep(i,,SZ(c)) c[i]=(mod-c[i])%mod;
        return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
    }
};

int main() {
    while(~scanf("%lld",&n)){
        printf("%d\n",linear_seq::gao(VI{,,,,,,,},n-));
    }
}