[机器学习&数据挖掘]SVM---软间隔最大化

根据上个硬间隔最大化已经知道，在解决线性可分数据集的分类问题时，求得拉格朗日乘子、w、b就得到分离超平面，然后就可以进行分类，软间隔最大化是针对非线性可分的数据集，因为并不是数据集在可分的时候会出现一些个别的点不能够被正确划分，而被划分到另一类中，软间隔最大化就是对目标函数加上一个惩罚项，或者说是松弛变量，这样可以稍微灵活的进行分类，因此需要对上边所说的问题、公式进行一些调整。

因此原始问题就变成如下：

　　　　　　　　　　　　　　　　　　　　

其中是松弛变量，C是惩罚参数，一般由应用问题决定，C增大对误分类的惩罚增大，C减小对误分类的惩罚减小。

对偶问题则变成如下：

　　　　　　　　　　　　　　　　　　　　

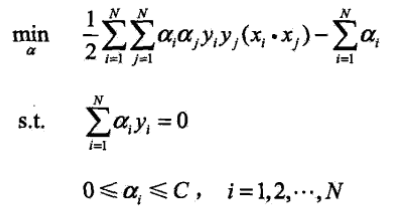
接下来的w和b的求解公式便与硬间隔最大化是相同的如下：