LeetCode题解之 Letter Case Permutation

1、题目描述

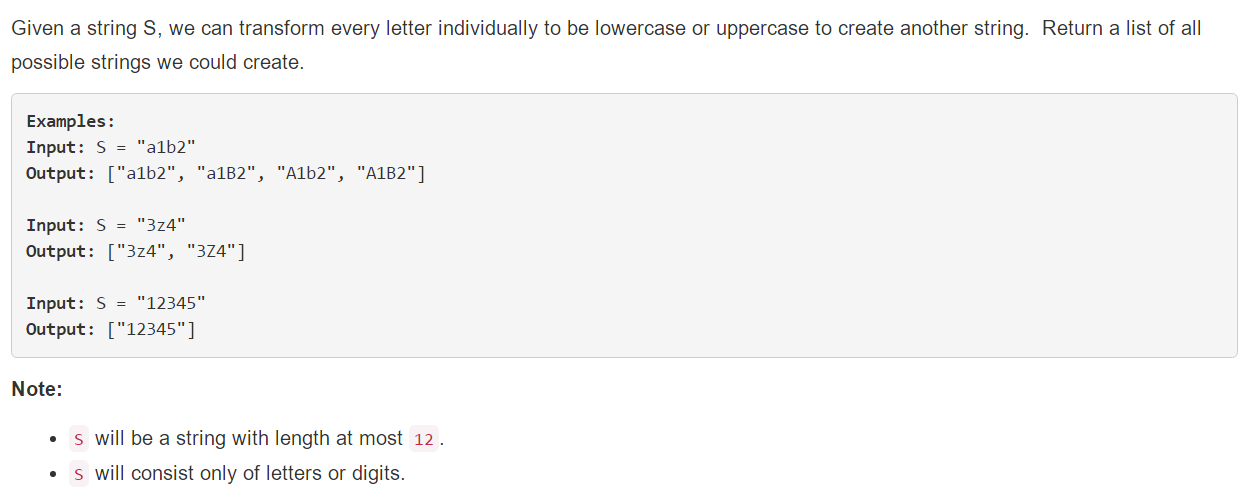
2、问题分析

可以使用递归的方法解决，参考了别人的答案才写出来的。

3、代码

  vector<string> letterCasePermutation(string S) {
         vector<string> res ;
         recursion( S,res, );
         return res;

     }

     void recursion(string & s , vector<string> &r ,int p){
         if( p == s.size() ){
             r.push_back( s );
             return ;
         }

         recursion( s ,r ,p+ );
         if( isalpha( s[p] )){
            if( islower( s[p] ) ){
                 s[p] += 'A' - 'a';
             }else if( isupper( s[p] ) ){
                 s[p] += 'a' - 'A';
             }
             recursion( s,r,p+ );
         }
     }