深度优先搜索DFS和广度优先搜索BFS

DFS简介

　　深度优先搜索，一般会设置一个数组visited记录每个顶点的访问状态，初始状态图中所有顶点均未被访问，从某个未被访问过的顶点开始按照某个原则一直往深处访问，访问的过程中随时更新数组visited，碰到已访问的顶点则回溯到前一顶点按原则选择另一条路径走，如果无路可走时则再次回溯，坚持此原则（总之就是有路走就走，无路走就回溯），最后会回溯到初始顶点。然后从下一个未被访问过的顶点开始，重复上述过程，直到所有顶点都被访问完。

BFS简介

　　广度优先搜索，一般会使用一个队列que，从起点开始，把起点放入que，然后把它拿出来，把它的邻节点们依次放进去，然后对这些邻节点们做重复的操作，直到队列里没有顶点，也就是所有顶点被访问完了。BFS像是一个从起点开始，到邻节点，再到邻节点，由内向外不断扩散的过程。

举例解释

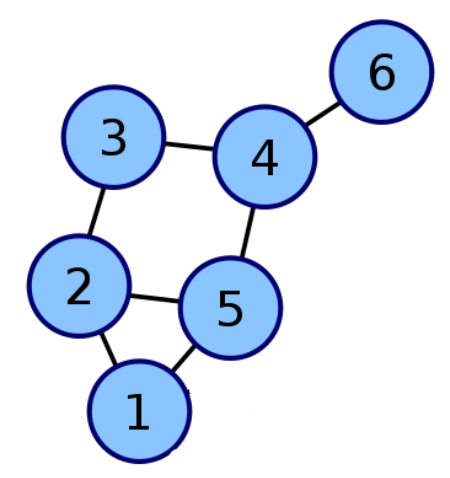
从1开始去寻找5

DFS：

　　原则：优先选择左手边

　　过程：1-2-3-4-6-4-5

BFS：

　　队列情况：1

　　　　　　　2、5

　　　　　　　5、3

　　　　　　　5出来则找到

遍历图中所有点

DFS：

　　原则：优先选择左手边

　　过程：1-2-3-4-6-4-5

BFS：

　　队列情况：1

　　　　　　　2、5

　　　　　　　5、3

　　　　　　　3、4

　　　　　　　4

　　　　　　　6

　　　　　　　6出来则结束