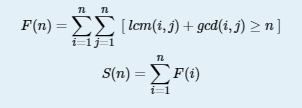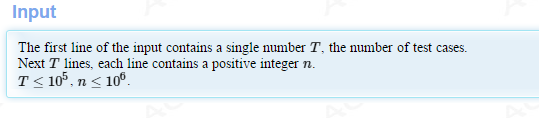【HDU 5382】 GCD?LCM! (数论、积性函数)
GCD?LCM!
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 316 Accepted Submission(s): 200
OutputT lines, find S(n) mod 258280327.Sample Input8
1
2
3
4
10
100
233
11037Sample Output1
5
13
26
289
296582
3928449
213582482AuthorSXYZSource
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define Maxn 1000010
#define Mod 258280327 int pri[Maxn],pl,g[Maxn],t[Maxn],f[Maxn];
bool vis[Maxn]; void init()
{
memset(vis,,sizeof(vis));
pl=;g[]=;
for(int i=;i<=Maxn-;i++)
{
if(!vis[i]) pri[++pl]=i,g[i]=;
for(int j=;j<=pl;j++)
{
if(pri[j]*i>Maxn-) break;
vis[i*pri[j]]=;
if(i%pri[j]==) g[i*pri[j]]=g[i];
else g[i*pri[j]]=*g[i]%Mod;
if(i%pri[j]==) break;
}
}
for(int i=;i<=Maxn-;i++)
{
for(int j=i;j<=Maxn-;j+=i)
{
t[j]=(t[j]+g[j/i-])%Mod;
}
}
for(int i=;i<=Maxn-;i++) f[i]=(f[i-]+(*i-)-t[i-])%Mod;
for(int i=;i<=Maxn-;i++) f[i]=((f[i]+f[i-])%Mod+Mod)%Mod;
} int main()
{
init();
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
printf("%d\n",f[n]);
}
return ;
}
【有一点点容斥的东东在么?】
2017-04-27 15:28:52
【HDU 5382】 GCD?LCM! (数论、积性函数)的更多相关文章
- 2015多校第8场 HDU 5382 GCD?LCM! 数论公式推导
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5382 题意:函数lcm(a,b):求两整数a,b的最小公倍数:函数gcd(a,b):求两整数a,b的最 ...
- 数学--数论--Hdu 1452 Happy 2004(积性函数性质+和函数公式+快速模幂+乘法逆元)
Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your ...
- hdu 5382 GCD?LCM! - 莫比乌斯反演
题目传送门 传送门I 传送门II 题目大意 设$F(n) = \sum_{i = 1}^{n}\sum_{j = 1}^{n}\left [ [i, j] + (i, j) \geqslant n \ ...
- hdu 5382 GCD?LCM!
先考虑化简f函数 发现,f函数可以写成一个递归式,化简后可以先递推求出所有f函数的值, 所以可以先求出所有S函数的值,对于询问,O(1)回答 代码: //File Name: hdu5382.cpp ...
- 积性函数,线性筛入门 HDU - 2879
HDU - 2879HeHe 题意:He[N]为[0,N−1]范围内有多少个数满足式子x2≡x (mod N),求HeHe[N]=He[1]×……×He[N] 我是通过打表发现的he[x]=2k,k为 ...
- 数学--数论--HDU 5382 GCD?LCM?(详细推导,不懂打我)
Describtion First we define: (1) lcm(a,b), the least common multiple of two integers a and b, is the ...
- HDU 1452 Happy 2004 (逆元+快速幂+积性函数)
G - Happy 2004 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Subm ...
- HDU 1452 Happy 2004(因子和的积性函数)
题目链接 题意 : 给你一个X,让你求出2004的X次方的所有因子之和,然后对29取余. 思路 : 原来这就是积性函数,点这里这里这里,这里讲得很详细. 在非数论的领域,积性函数指所有对于任何a,b都 ...
- Mobius反演与积性函数前缀和演学习笔记 BZOJ 4176 Lucas的数论 SDOI 2015 约数个数和
下文中所有讨论都在数论函数范围内开展. 数论函数指的是定义域为正整数域, 且值域为复数域的函数. 数论意义下的和式处理技巧 因子 \[ \sum_{d | n} a_d = \sum_{d | n} ...
随机推荐
- [Java] Servlet工作原理之二:Session与Cookie
(未完成) 一.Cookie与Session的使用简介 1 Cookie Cookie 用于记录用户在一段时间内的行为,它有两个版本:Version 0 和 Version 1,分别对应两种响应头 S ...
- np.random.rand均匀分布随机数和np.random.randn正态分布随机数函数使用方法
np.random.rand用法 觉得有用的话,欢迎一起讨论相互学习~Follow Me 生成特定形状下[0,1)下的均匀分布随机数 np.random.rand(a1,a2,a3...)生成形状为( ...
- C语言复习---获取最小公倍数(公式法:两个数相乘等于最小公倍数乘以最大公约数)
公式法:两个数相乘等于最小公倍数乘以最大公约数 #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib ...
- Spring Boot 源码分析 数据源 + Mybatis 配置
公司今年开始使用 Spring Boot 开发,当然使用 Spring Boot 也是大势所趋,尤其是现在微服务的趋向,当然是选择基于Spring Boot 的 Spring Cloud.(所谓的 S ...
- AngularJS 启程
<!DOCTYPE html> <html lang="en" ng-app> <head> <meta charset="UT ...
- python学习笔记7-网络编程
import urllib.request import json,requests #urlib模块,不常用 url = 'http://api.nnzhp.cn/api/user/stu_info ...
- javascript构造函数强制使用new
如果有时候我们忘记对构造函数使用new的话,构造函数的this将指向window function Person(){ this.name = 'Julie'; } var good_moring = ...
- 工欲善其事必先利其器,用Emmet提高HTML编写速度
HTML代码写起来很费事,因为它的标签多. 一种解决方法是采用模板,在别人写好的骨架内,填入自己的内容.还有一种很炫的方法----简写法. 常用的简写法,目前主要是Emmet和Haml两种.这两种简写 ...
- Dream------Hbase--0.94版本和0.98/1.X版本api变动
Dream------Hbase--0.94版本和0.98/1.X版本api变动 网上好多说getQualifier.getValue.getRow被..Array代替了,其实并不是的. 1. Int ...
- 【干货】linux系统信息收集 ----检测是否被恶意程序执行了危险性命令
这些实战完全可以练习以下命令,已经找到需要观察的交互点,真实工作的时候,把数据都导入到自己U盘或者工作站内. 在kali 或者centos下训练都一样,关于kali教学,这里推荐掌控安全团队的课程:掌 ...