15 图-图的遍历-基于邻接矩阵实现的BFS与DFS算法
算法分析和具体步骤解说直接写在代码注释上了
TvT 没时间了等下还要去洗衣服 就先不赘述了
有不明白的欢迎留言交流!(估计是没人看的了)
直接上代码:
#include<stdio.h>
#include<queue>
#include<iostream>
using namespace std;
typedef struct{
int Vex[];//顶点表
int Edge[][];
int vexnum,arcnum;
}MGraph;
bool visited[];
void printGraph(MGraph &G)
{
cout<<"Show the Graph."<<endl;
cout<<"----------------------------"<<endl;
for(int i=;i<;i++){
for(int j=;j<;j++)
{
cout<<" "<<G.Edge[i][j]<<" ";
}
cout<<endl;
}
cout<<"----------------------------"<<endl;
cout<<"There are "<<G.arcnum<<" arcs in the Graph!"<<endl;
cout<<"Arcs are listed as follow:"<<endl;
for(int i=;i<;i++){
for(int j=;j<;j++)
{
if(G.Edge[i][j]==)
cout<<i<<"-->"<<j<<endl;
}
}
}
int initGraph(MGraph &G)
{
G.vexnum=;
G.arcnum=;
for(int i=;i<;i++)
for(int j=;j<;j++)
{
G.Edge[i][j]=;
}
cout<<"input the relation of a pair of dots (A,B) to build a graph.(0<A,B<10)"<<endl;
cout<<"End up with data(0,0)"<<endl;
int a,b;
cin>>a>>b;
while(a!=&&b!=){
G.arcnum++;
G.Edge[a][b]=;
cin>>a>>b;
}
cout<<"successful."<<endl;
printGraph(G);
}
bool isNeibour(MGraph &G,int a,int b)
{
if(G.Edge[a][b]==)
return true;
else return false;
}
int firstNeighbor(MGraph &G,int v)
{
int pos=-;
for(int i=;i<G.vexnum;i++)
{
if((G.Edge[v][i]==))
{pos=i;break;}
}
return pos;
}
int nextNeighbor(MGraph &G,int v,int w)
{
int pos=-;
for(int i=w+;i<G.vexnum;i++)
{
if((G.Edge[v][i]==))
{
pos=i;break;
}
}
return pos;
}
void visit(int v)
{
visited[v]=true;
cout<<v<<" ";
}
queue<int> Q;
void bfs(MGraph G,int v)
{
visit(v);
Q.push(v);
int now;
while(!Q.empty())
{
now=Q.front();
Q.pop();
for(int w=firstNeighbor(G,now);w>=;w=nextNeighbor(G,now,w))
{
if(!visited[w])
{
visit(w);
Q.push(now);
}
}
}
}
void BFS(MGraph &G)
{
for(int i=;i<G.vexnum;i++)
visited[i]=false;
for(int i=;i<G.vexnum;i++)
{
if(!visited[i])
bfs(G,i);
}
}
/*DFS 深度优先搜索*/
/*类似于树的先序遍历
其搜索策略:尽可能【深】地搜索一个图。
遍历思想:
从一个起始顶点v出发,访问与v邻接但未被访问的任一顶点a→继续访问a顶点的下一未被访问的顶点b→……→无法再向下访问时依次退回到最近被访问的顶点
直到所有顶点都被访问为止
*/
void dfs(MGraph &G,int v)
{
visit(v);
int w;
for(w=firstNeighbor(G,v);w>=;w=nextNeighbor(G,v,w))
{
if(!visited[w])
{
dfs(G,w);
}
}
}
void DFS(MGraph &G)
{
for(int i=;i<G.vexnum;i++)
{
visited[i]=false;
}
for(int i=;i<G.vexnum;i++)
{
if(!visited[i])
dfs(G,i);
}
}
int main()
{
MGraph P;
initGraph(P);
cout<<"test of BFS:"<<endl;
BFS(P);
cout<<endl;
cout<<"test of DFS:"<<endl;
DFS(P);
return ;
}
附一张运行截图
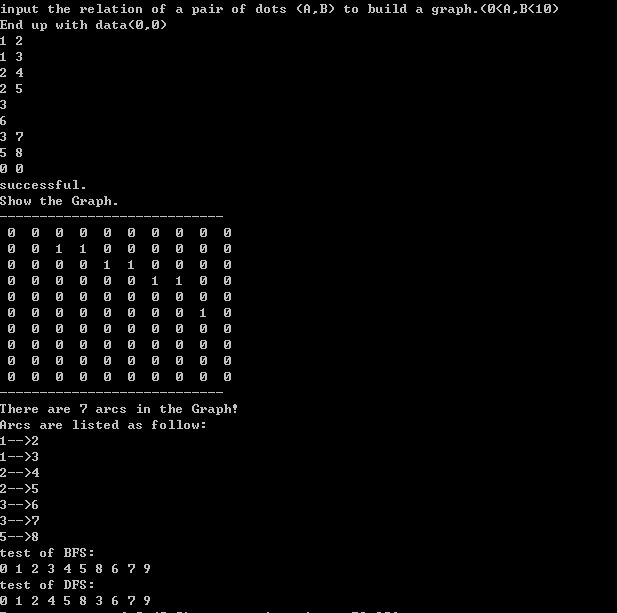
15 图-图的遍历-基于邻接矩阵实现的BFS与DFS算法的更多相关文章
- 图的全部实现(邻接矩阵 邻接表 BFS DFS 最小生成树 最短路径等)
1 /** 2 * C: Dijkstra算法获取最短路径(邻接矩阵) 3 * 6 */ 7 8 #include <stdio.h> 9 #include <stdlib.h> ...
- 数据结构实验之图论二:图的深度遍历(SDUT 2107)(简单DFS)
题解:图的深度遍历就是顺着一个最初的结点开始,把与它相邻的结点都找到,也就是一直往下搜索直到尽头,然后在顺次找其他的结点. #include <bits/stdc++.h> using n ...
- 图的基本操作(基于邻接矩阵):图的构造,深搜(DFS),广搜(BFS)
#include <iostream> #include <stdio.h> #include <cstdlib> #include <cstring> ...
- 基于邻接矩阵的深度优先搜索(DFS)
题目:http://acm.sdut.edu.cn/sdutoj/showproblem.php?pid=2107&cid=1186 #include<stdio.h> #incl ...
- 邻接矩阵实现Dijkstra算法以及BFS与DFS算法
//============================================================================ // Name : MatrixUDG.c ...
- PTA 邻接矩阵存储图的深度优先遍历
6-1 邻接矩阵存储图的深度优先遍历(20 分) 试实现邻接矩阵存储图的深度优先遍历. 函数接口定义: void DFS( MGraph Graph, Vertex V, void (*Visit)( ...
- 算法学习 - 图的广度优先遍历(BFS) (C++)
广度优先遍历 广度优先遍历是非经常见和普遍的一种图的遍历方法了,除了BFS还有DFS也就是深度优先遍历方法.我在我下一篇博客里面会写. 遍历过程 相信每一个看这篇博客的人,都能看懂邻接链表存储图. 不 ...
- C语言实现邻接矩阵创建无向图&图的深度优先遍历
/* '邻接矩阵' 实现无向图的创建.深度优先遍历*/ #include <stdio.h> #include <stdlib.h> #define MaxVex 100 // ...
- 数据结构与算法之PHP用邻接表、邻接矩阵实现图的广度优先遍历(BFS)
一.基本思想 1)从图中的某个顶点V出发访问并记录: 2)依次访问V的所有邻接顶点: 3)分别从这些邻接点出发,依次访问它们的未被访问过的邻接点,直到图中所有已被访问过的顶点的邻接点都被访问到. 4) ...
随机推荐
- python_day1_python简单介绍
一.python解释器的种类 我们都知道python是一种解释型的语言,那python在执行的过程中必须要通过解释器来执行,那python的解释器到底分为哪些呢? 1.Cpython CPython是 ...
- 30条SQL查询优化原则
在我们平常的SQL查询中,其实我们有许多应该注意的原则,以来实现SQL查询的优化,本文将为大家介绍30条查询优化原则. 首先应注意的原则 1.对查询进行优化,应尽量避免全表扫描,首先应考虑在 wher ...
- shell工具-sort
sort sort命令是在Linux里非常有用,它将文件进行排序,并将排序结果标准输出 基本语法 sort [选项] [参数] 选项说明 选项 说明 -n 依照数值大小排序 -r 以相反的顺序排序 - ...
- JVM虚拟机---本地接口(我还不太会)
转载http://www.newhua.com/2008/0328/33542_2.shtml Java本地接口(Java Native Interface (JNI))允许运行在Java虚拟机(Ja ...
- AngularJS 表单数据验证及错误信息提示
一.表单验证基本原理 表单验证包括两个主题: 定义验证规则,验证数据有效性. 显示验证结果,把验证结果以友好的方式显示给用户. H5内置一些验证功能,并会显示内置的错误提示信息,先要禁用它,在< ...
- iOS 应用如何完全支持 IPv6-ONLY 网络?
iOS 应用如何完全支持 IPv6-ONLY 网络?¶ 警告 您当前查看的页面是未经授权的转载! 如果当前版本排版错误,请前往查看最新版本:http://www.cnblogs.com/qin-nz/ ...
- JS学习笔记2_面向对象
1.对象的定义 ECMAScript中,对象是一个无序属性集,这里的“属性”可以是基本值.对象或者函数 2.数据属性与访问器属性 数据属性即有值的属性,可以设置属性只读.不可删除.不可枚举等等 访问器 ...
- XAML 调试工具 不见了?
XAML调试工具不见了怎么办? 1.调试---> 选项---> 选中 启用XAML的UI调试工具 2.调试---> 选项---> 禁用 使用托管兼容模式 欧了!
- [面试题目]IT面试中的一些基础问题
1. 面向对象的特征 继承,封装,多态 2. 重写和重载的区别 重写:在继承当中,子类重写父类的函数,函数声明完全一样,只是函数里面的操作不一样,这样叫做重写. 重载:与多态无关,即两个函数名一样的成 ...
- SQL注入之PHP-MySQL实现手工注入-数字型
SQL注入,就是通过把SQL命令插入到Web表单提交或输入域名或页面请求的查询字符串,最终达到欺骗服务器执行恶意的SQL命令.具体来说,它是利用现有应用程序,将(恶意的)SQL命令注入到后台数据库引擎 ...
