[hihoCoder] 骨牌覆盖问题·一

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：
我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？
举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：

提示：骨牌覆盖

提示：如何快速计算结果

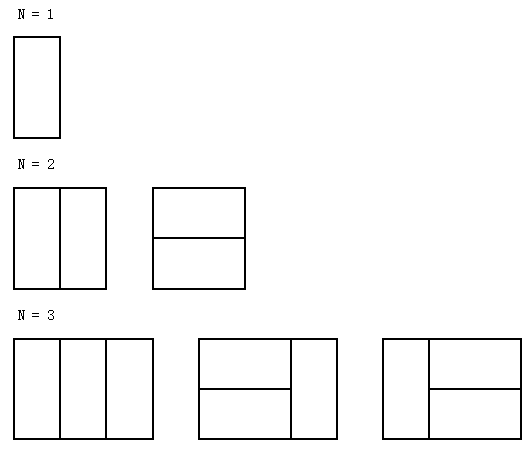
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 19999997

样例输入

62247088

样例输出

17748018

当N很小的时候，我们直接通过递推公式便可以计算。当N很大的时候，只要我们的电脑足够好，我们仍然可以直接通过递推公式来计算。
但是我们学算法的，总是这样直接枚举不是显得很Low么，所以我们要用一个好的算法来加速(装X)。
事实上，对于这种线性递推式，我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列，我们希望找到一个2x2的矩阵M，使得(a, b) x M = (b, a+b)，其中(a, b)和(b, a+b)都是1x2的矩阵。
显然，只需要取M = [0, 1; 1, 1]就可以了：

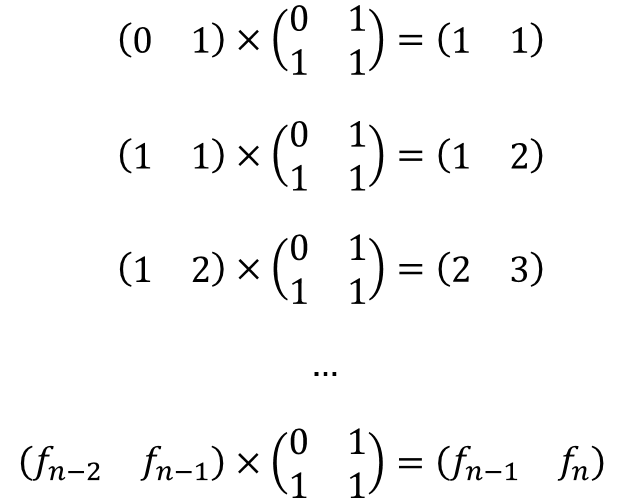
进一步得到：

那么接下来的问题是，能不能快速的计算出M^n？我们先来分析一下幂运算。由于乘法是满足结合律的，所以我们有：

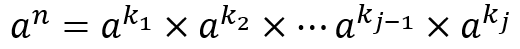
不妨将k[1]..k[j]划分的更好一点？

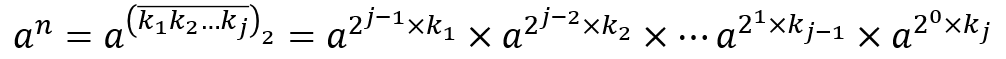
其中(k[1],k[2]...k[j])2表示将n表示成二进制数后每一位的数字。上面这个公式同时满足这样一个性质：

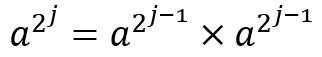
结合这两者我们可以得到一个算法：
1. 先计算出所有的{a^1, a^2, a^4 ... a^(2^j)}，因为该数列满足递推公式，时间复杂度为O(logN)
2. 将指数n二进制化，再利用公式将对应的a^j相乘计算出a^n，时间复杂度仍然为O(logN)
则总的时间复杂度为O(logN)
这种算法因为能够在很短时间内求出幂，我们称之为“快速幂”算法。

 #include <iostream>
 #include <vector>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 const ll MOD = ;

 struct matrix {
     ll a, b, c, d;
     matrix() : a(), b(), c(), d() {}
     matrix operator * (const matrix &m) const {
         matrix tmp;
         tmp.a = (a * m.a + b * m.c) % MOD;
         tmp.b = (a * m.b + b * m.d) % MOD;
         tmp.c = (c * m.a + d * m.c) % MOD;
         tmp.d = (c * m.b + d * m.d) % MOD;
         return tmp;
     }
 };

 matrix pow(const matrix &a, int n) {
     matrix tmp;
     if (n ==  || n == ) return tmp;
     tmp = pow(a, n / );
     if (n & ) {
         tmp = tmp * tmp * a;
     } else {
         tmp = tmp * tmp;
     }
     return tmp;
 }

 int main() {
     ll n;
     matrix a, b;
     while (cin >> n) {
         b = pow(a, n);
         cout << b.d << endl;
     }
     return ;
 }