齐次坐标(Homogeneous Coordinates)

原文：http://blog.163.com/m_note/blog/static/208197045201272341230195/

齐次坐标(Homogeneous Coordinates) 
问题: 两条平行线会相交

铁轨在无限远处相交于一点
在欧几里得几何空间里，两条平行线永远都不会相交。但是在投影空间中，如右图中的两条铁轨在地平线处却是会相交的，因为在无限远处它们看起来相交于一点。
在欧几里得（或称笛卡尔）空间里描述2D/3D 几何物体是很理想的，但在投影空间里面却并不见得。 我们用 (x, y) 表示笛卡尔空间中的一个 2D 点，而处于无限远处的点 (∞,∞) 在笛卡尔空间里是没有意义的。投影空间里的两条平行线会在无限远处相交于一点，但笛卡尔空间里面无法搞定这个问题（因为无限远处的点在笛卡尔空间里是没有意义的），因此数学家想出齐次坐标这个点子来了。
解决办法: 其次坐标由 August Ferdinand M bius 提出的齐次坐标（Homogeneous coordinates）让我们能够在投影空间里进行图像和几何处理，齐次坐标用 N + 1个分量来描述 N 维坐标。比如，2D 齐次坐标是在笛卡尔坐标(X, Y)的基础上增加一个新分量 w，变成(x, y, w)，其中笛卡尔坐标系中的大X，Y 与齐次坐标中的小x，y有如下对应关系：
X = x/w
Y = y/w 
笛卡尔坐标中的点 (1, 2) 在齐次坐标中就是 (1, 2, 1) 。如果这点移动到无限远(∞,∞)处，在齐次坐标中就是 (1, 2, 0) ，这样我们就避免了用没意义的"∞" 来描述无限远处的点。
为什么叫齐次坐标？前面提到，我们分别用齐次坐标中的 x 和 y 除以 w 就得到笛卡尔坐标中的 x 和 x，如图所示：

 
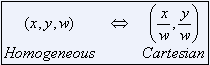
仔细观察下面的转换例子，可以发现些有趣的东西：

 
上图中，点 (1, 2, 3), (2, 4, 6) 和 (4, 8, 12) 对应笛卡尔坐标中的同一点 (1/3, 2/3)。 任意数量积的(1a, 2a, 3a) 始终对应于笛卡尔坐标中的同一点 (1/3, 2/3)。因此这些点是“齐次”的，因为他们始终对应于笛卡尔坐标中的同一点。换句话说，齐次坐标描述缩放不变性（scale invariant）。
证明: 两平行线可以相交笛卡尔坐标系中，对于如下两个直线方程：

 
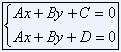
如果 C ≠ D，以上方程组无解；如果 C = D，那这两条线就是同一条线了。
下面我们用 x/w, y/w 代替 x, y 放到投影空间里来求解：

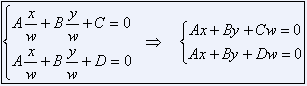
现在我们就可以在 C ≠ D 的情况得到一组解 (x, y, 0)，代入得 (C - D)w = 0，因为 C ≠ D，所以 w = 0。因而，两条平行线相交于投影空间中无限远处的一点 (x, y, 0)。
齐次坐标在计算机图形学中是有用的，将 3D 场景投影到 2D 平面的过程中就用到它了。