学习笔记：A*算法

简易地图　　　　　　　　　

如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.

二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上.

寻路步骤　　　　　　　　　　

1. 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.

2. 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.

3. 从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格

图中浅绿色描边的方块表示已经加入 "开启列表" 等待检查. 淡蓝色描边的起点 A 表示已经放入 "关闭列表" , 它不需要再执行检查.

从 "开启列表" 中找出相对最靠谱的方块, 什么是最靠谱? 它们通过公式 F=G+H 来计算.

        F = G + H

G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动).

H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 这里我们设定只可以上下左右移动).

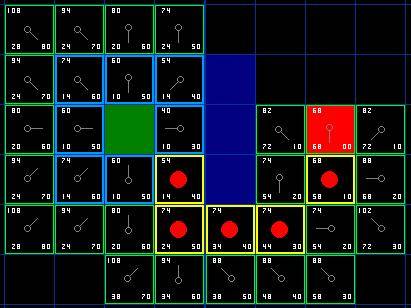
我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 FGH, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的结果一样?

从 "开启列表" 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 然后对它进行如下处理:

4. 把它从 "开启列表" 中删除, 并放到 "关闭列表" 中.

5. 检查它所有相邻并且可以到达 (障碍物和 "关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在 "开启列表" 里的话, 将它们加入 "开启列表", 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 "父方格" 为 C.

6. 如果某个相邻方格 D 已经在 "开启列表" 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 "父方格" 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.

如图, 我们选中了 C 因为它的 F 值最小, 我们把它从 "开启列表" 中删除, 并把它加入 "关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到 "关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.

然后我们继续从 "开启列表" 中找出 F 值最小的, 但我们发现 C 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.

D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 "开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)

就这样, 我们从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...

那么什么时候停止呢? —— 当我们发现 "开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.

如何找回路径　　　　　　　

如上图所示, 除了起始方块, 每一个曾经或者现在还在 "开启列表" 里的方块, 它都有一个 "父方块", 通过 "父方块" 可以索引到最初的 "起始方块", 这就是路径.

将整个过程抽象　　　　　　

把起始格添加到 "开启列表"
do

{

       寻找开启列表中F值最低的格子, 我们称它为当前格.

       把它切换到关闭列表.

       对当前格相邻的8格中的每一个

          if (它不可通过 || 已经在 "关闭列表" 中)

          {

                什么也不做.

           }

          if (它不在开启列表中)

          {

                把它添加进 "开启列表", 把当前格作为这一格的父节点, 计算这一格的 FGH

          if (它已经在开启列表中)

          {

                if (用G值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)

                    {

                            把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值.

                    }

} while( 目标格已经在 "开启列表", 这时候路径被找到)

如果开启列表已经空了, 说明路径不存在.

最后从目标格开始, 沿着每一格的父节点移动直到回到起始格, 这就是路径.