【cs231n】图像分类-Linear Classification线性分类

【学习自CS231n课程】

转载请注明出处：http://www.cnblogs.com/GraceSkyer/p/8824876.html

　　之前介绍了图像分类问题。图像分类的任务，就是从已有的固定分类标签集合中选择一个并分配给一张图像。我们还介绍了k-Nearest Neighbor （k-NN）分类器，该分类器的基本思想是通过将测试图像与训练集带标签的图像进行比较，来给测试图像打上分类标签。k-Nearest Neighbor分类器存在以下不足：

分类器必须记住所有训练数据并将其存储起来，以便于未来测试数据用于比较。这在存储空间上是低效的，数据集的大小很容易就以GB计。
对一个测试图像进行分类需要和所有训练图像作比较，算法计算资源耗费高。

　　我们将实现一种更强大的方法来解决图像分类问题，该方法可以自然地延伸到神经网络和卷积神经网络上。这种方法主要有两部分组成：

评分函数（score function），它是原始图像数据到类别分值的映射。
损失函数（loss function），它是用来量化预测分类标签的得分与真实标签之间一致性的。该方法可转化为一个最优化问题，在最优化过程中，将通过更新评分函数的参数来最小化损失函数值。

从图像到标签分值的参数化映射

　　该方法的第一部分就是定义一个评分函数，这个函数将图像的像素值映射为各个分类类别的得分，得分高低代表图像属于该类别的可能性高低。下面会利用一个具体例子来展示该方法。

　　现在假设有一个包含很多图像的训练集 $x_i\in R^D$ ，每个图像都有一个对应的分类标签 $y_i$ 。这里 $i=1,2...N$ 并且 $y_i\in 1...K$ 。这就是说，我们有N个图像样例，每个图像的维度是D，共有K种不同的分类。

　　举例来说，在CIFAR-10中，我们有一个N=50000的训练集，每个图像有D=32x32x3=3072个像素（每个图像都是32*32像素，每幅图形有3个彩色通道），而K=10，这是因为图片被分为10个不同的类别（狗，猫，汽车等）。我们现在定义评分函数为： $f:R^D\to R^K$ ，该函数是原始图像像素到分类分值的映射。

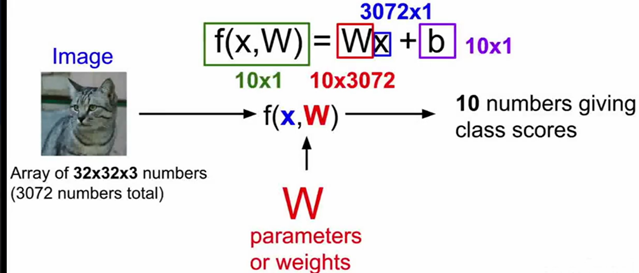
线性分类器函数形式

　　在本模型中，我们从最简单的概率函数开始，一个线性映射：

$\displaystyle f(x_i,W,b)=Wx_i+b$

　　在上面的公式中，假设每个图像数据都被拉长为一个长度为D的列向量，大小为[D x 1]。其中大小为[K x D]的矩阵W和大小为[K x 1]列向量b为该函数的参数（parameters）。还是以CIFAR-10为例， $x_i$ 就包含了第i个图像的所有像素信息，这些信息被拉成为一个[3072 x 1]的列向量，W大小为[10x3072]，b的大小为[10x1]。因此，3072个数字（原始像素数值）输入函数，函数输出10个数字（不同分类得到的分值）。

　　参数W被称为权重（weights），有时也叫θ。

　　参数b被称为偏差向量（bias vector），这是因为它影响输出数值，但是并不和原始数据 $x_i$ 产生关联。它不与训练数据交互，而只会给我们一些仅针对一类的数据独立的偏好值。【所以，如果你的数据集是不平衡的，即猫的数量多于狗时，那么猫对应的偏差元素就会比其他的要高。】

　　在实际情况中，人们常常混用权重和参数这两个术语。

需要注意的几点：

首先，一个单独的矩阵乘法 $Wx_i$ 就高效地并行评估10个不同的分类器（每个分类器针对一个分类），其中每个类的分类器就是W的一个行向量。
注意我们认为输入数据 $(x_i,y_i)$ 是给定且不可改变的，但参数W和b是可控制改变的。我们的目标就是通过设置这些参数，使得计算出来的分类分值情况和训练集中图像数据的真实类别标签相符。在接下来的课程中，我们将详细介绍如何做到这一点，但是目前只需要直观地让正确分类的分值比错误分类的分值高即可。
该方法的一个优势是训练数据是用来学习到参数W和b的，一旦训练完成，训练数据就可以丢弃，留下学习到的参数即可。这是因为一个测试图像可以简单地输入函数，并基于计算出的分类分值来进行分类。
最后，注意只需要做一个矩阵乘法和一个矩阵加法就能对一个测试数据分类，这比k-NN中将测试图像和所有训练数据做比较的方法快多了。

理解线性分类器

　　线性分类器计算图像中3个颜色通道中所有像素的值与权重的矩阵乘，从而得到分类分值。根据我们对权重设置的值，对于图像中的某些位置的某些颜色，函数表现出喜好或者厌恶（根据每个权重的符号而定）。举个例子，可以想象“船”分类就是被大量的蓝色所包围（对应的就是水）。那么“船”分类器在蓝色通道上的权重就有很多的正权重（它们的出现提高了“船”分类的分值），而在绿色和红色通道上的权重为负的就比较多（它们的出现降低了“船”分类的分值）。

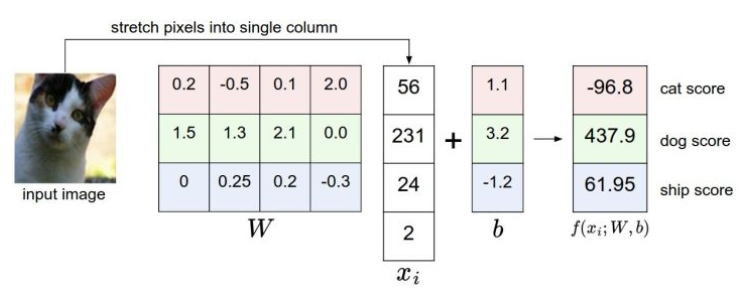
　　上面为一个将图像映射到分类分值的例子。为了便于可视化，假设图像只有4个像素（都是黑白像素，这里不考虑RGB通道），有3个分类（红色代表猫，绿色代表狗，蓝色代表船，注意，这里的红、绿和蓝3种颜色仅代表分类，和RGB通道没有关系）。首先将图像像素拉伸为一个列向量，与W进行矩阵乘，再加上偏差向量，然后得到各个分类的分值。需要注意的是，这个W一点也不好：猫分类的分值非常低。从上图来看，算法倒是觉得这个图像是一只狗。

将图像看做高维度的点

　　线性分类器的另一个观点是回归到图像，作为点和高维空间的概念，你可以想象成我们每一张图像都是类似高维空间中一个点的东西【即上面例子中，每张图像是3072维空间中的一个点。整个数据集就是一个点的集合，每个点都带有1个分类标签。】　　线性分类器在这些线性决策边界上尝试画一个线性分类面来划分一个类别和剩余其他类别。

　　既然定义每个分类类别的分值是权重和图像的矩阵乘，那么每个分类类别的分数就是这个空间中的一个线性函数的函数值。我们没办法可视化3072维空间中的线性函数，但假设把这些维度挤压到二维，那么就可以看看这些分类器在做什么了：

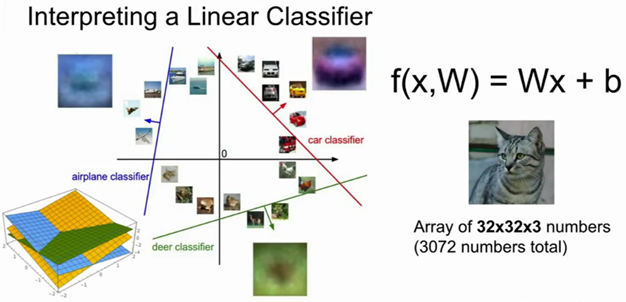
　　图像空间的示意图。其中每个图像是一个点，有3个分类器。以红色的汽车分类器为例，红线表示空间中汽车分类分数为0的点的集合，红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正，且线性升高。红线左边的点分值为负，且线性降低。　　

　　从上面可以看到，W的每一行都是一个分类类别的分类器。对于这些数字的几何解释是：如果改变其中一行的数字，会看见分类器在空间中对应的直线开始向着不同方向旋转。而偏差b，则允许分类器对应的直线平移。需要注意的是，如果没有偏差，无论权重如何，在 $x_i=0$ 时分类分值始终为0。这样所有分类器的线都不得不穿过原点。

将线性分类器看做模板匹配

　　关于权重W的另一个解释是它的每一行对应着一个分类的模板（有时候也叫作原型）。一张图像对应不同分类的得分，是通过使用内积（也叫点积）来比较图像和模板，然后找到和哪个模板最相似。从这个角度来看，线性分类器就是在利用学习到的模板，针对图像做模板匹配。从另一个角度来看，可以认为还是在高效地使用k-NN，不同的是我们没有使用所有的训练集的图像来比较，而是每个类别只用了一张图片（这张图片是我们学习到的，而不是训练集中的某一张），而且我们会使用（负）内积来计算向量间的距离，而不是使用L1或者L2距离。

　　下图例子中，我们已经提前训练好了一个线性分类器，下方就是我们数据集中训练得到的权值矩阵中的行向量对应于10个类别相关的可视化结果。左下角是飞机类别的模板，似乎由中间类似蓝色斑点状图形和蓝色背景组成，这样你会认为飞机的线性分类器可能在寻找蓝色图形和斑点状图形，然后这些行为使得这个分类器更像飞机。这就存在问题：线性分类器每个类别只能学习一个模板，如果这个类别出现了某种类型的变体，那么它将尝试求取所以不同的变体，所有那些不同的平均值，并且只使用一个单独的模板来识别其中的每一个类别。

线性分类器难以解决的问题：

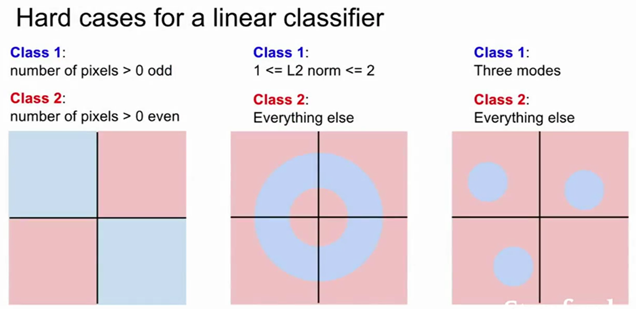
　　举个例子，下图中，在左边是假设我们有一个两个类别的数据集（这些数据全部也可能部分是人为的）我们的数据集有两类，蓝色和红色，如果你去画这些不同的决策，你能看到我们奇数像素点的蓝色类别在平面上有两个象限，甚至是两个相反的象限。所以我们没有办法能够绘制一条单独的直线来划分蓝色和红色，这是线性分类器的困境，也许归根结底这不是人工数据。实际上我们是在计算图像中动物或人类的奇偶数，而并非像素点。所以这种划分，奇数和偶数的划分问题是线性分类器通过传统方法难以解决的。

　　线性分类器难以解决的其他情况是 多分类问题。在右侧，可能我们蓝色类别存在于三个不同的象限，其他都是另外一个类别。目前还没有好方法可以在这两个类别之间绘制一条单独的线性边界，所以，任何时候当你有多模态数据，比如一个类别出现不同的领域空间中，这是另一个线性分类器可能有困境的地方。

参考：

https://www.bilibili.com/video/av17204303/?from=search&seid=6625954842411789830

https://zhuanlan.zhihu.com/p/20918580?refer=intelligentunit